I find a problem in the law of angular momentum conservation

Question

Consider a system of spring mass as shown in the figure.entire loop is free but only one nail is there at the point A... Initially the mass is at rest and then released. Assume that the spring is initially stretched and is in equilibrium in point C.

Now on the loop PQ (P=initial position of bead, Q=diametrically opposite) of the path the centre of the path is Point A. We are assuming that the loop is a massless, smooth rod. So the normal provided by the loop on the bead will pass through the axis. But the force of spring on the bead will be tangential to the path and the torque related to this force on the particle about the considered axis will be nonzero. Also no other forces are acting on the bead. So about the considered axis the angular momentum of the bead is changing. But if we analyse the entire loop+spring (massless)+bead system then there is no non-zero external torque acting on system. Since the only moving portion of the system is the bead angular momentum of the entire system is also changing. Note that the spring force is an internal force for the considered system. Where am I wrong ?

Answer 1

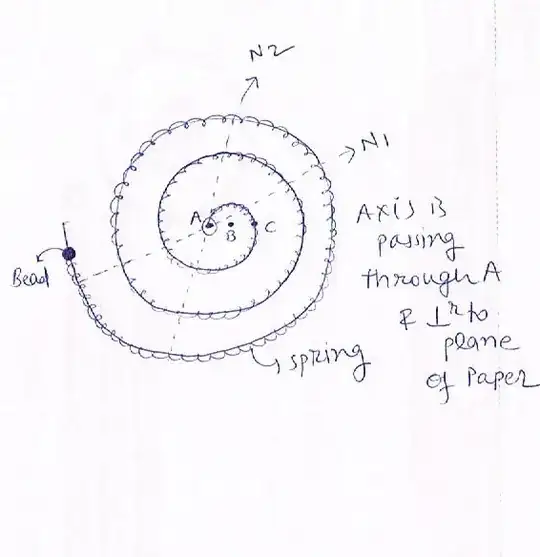
I think I initially misunderstood the question. I now believe there are three components here: a rigid massless rod in the shape of a spiral; a massless spring that is wound around the rod in a frictionless manner; and a bead at the end of the spring. The entire system is anchored at the point A by a single nail - thus, the system is free to rotate about this point A (it is a hinge, i.e. it fixes the position of the spiral at A, but not the direction).

Now it would be instructive to look at the forces on the system - remembering Newton's third law. You drew the following (I am simplifying the spiral to make the drawing clearer but the principle is the same):

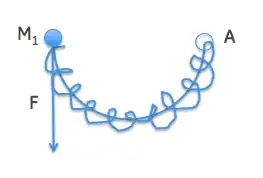
In reality, what you have is the following - at every point in the system there must be a force balance by Newton's third law:

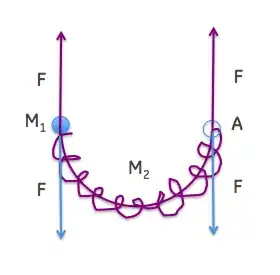
The spring is pulling "down" on the mass $M_1$ and on the nail $A$; the reaction is a net force of $2F$ on the "spring plus rod" system, to which I am assigning a mass $M_2$.

Now what would happen in a system with finite $M_2$ is the following:

Mass $M_1$ accelerates downward with $$a_1 =\frac{F}{M_1}$$

Mass $M_2$ accelerates upward with $$a_2 =\frac{2F}{M_2}$$

A short time later, the situation will look like this (I am sorry this is a messy drawing):

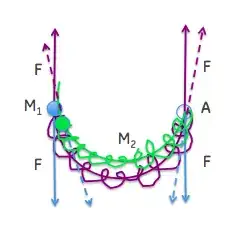
As you can see, the mass $M_1$ is moving down, and the mass $M_2$ is moving up; the direction of the forces is changing.

Now the relative velocities of the two parts of the system: bead, and {spring + rod} after a short time $\delta t$ (before the system has had chance to change shape significantly) is given by their relative masses from the two accelerations above:

$$ \frac{V_1}{V_2} = \frac{M_2}{2M_1}$$

(and these velocities are in opposite directions). Note that this expression shows conservation of angular momentum, since

$$ 2 M_1 V_1 = M_2 V_2$$

and the distance from the center of rotation (chosen to be at A) for $M_1$ is twice the distance for $M_2$ (projected onto the horizontal axis).

Now the only thing you have to do is take the limit of the above where $M_2$ is zero, and you see that angular momentum is conserved for this system.

Afterthought

The way I drew the spiral, it looked like a semicircle. In reality, one property of a spiral is that there has to be a radial component to the slope - so the force on mass $M_1$ is really not just tangential (as I drew it in the initial drawing), but it has both a tangential and a radial (inward) component. This shows that there is a force available for accelerating the mass inwards from the moment the system is released. The other aspects of the above description are unchanged - although it's slightly trickier to convince yourself of the balance of forces on the light rod when it has arbitrary shape. But the same argument holds as before: when the mass of rod+spring tends to zero, it will move instantaneously in a direction that opposes tangential motion by $M_1$, thus conserving angular momentum.

one more thought

I just re-read where you state "since the only thing moving is the bead". This could be read as meaning that the rod is fixed - in other words, that the point A is fixed such that the rod doesn't rotate about A. In that case there will be a torque at A which imparts angular momentum to the rod-spring-bead system on the one hand, and an equal and opposite angular momentum on the rest of the universe - in other words, with this kind of coupling you cannot consider the system "isolated".

Answer 2

Well lets hope I understood it correctly.

First of all since this is a horizontal loop and your bead is attached to the spring it would and should not touch the loop at all! (We are just solving the problem ideally, real life is tough) So lets throw out the Normals from our view.

Now you haven't mentioned whether you have your loop fixed to a table or absolutely free in space! So I'll consider two cases.

Case 1: Your loop is absolutely free in space If your loop is free in space and then you compress the spring and release, there is nothing to stop the loop from rotating in other direction accordingly to balance angular momentum. Keep in mind if you fix the loop with just one nail either at P or Q, even then the loop will rotate!

Case 2: Your loop has been fixed to a table by two nails at ends Well in this case your loop will not rotate to balance the angular momentum, but check out the normals from the nails. When the spring pushes the bead forward it alsi pushes the nail at point P tangentially back, which would be met by an equivalent normal which would then provide you your non-zero torque!

I would suggest you to experiment with it, for the first case compress the spring and release the system on the floor, even slight rotation of the whole system in opp direction would be proof of case 1. Case 2 can be tested as described.

Answer 3

In the ideal system you are imagining (mass less spring of fixed shape, friction free, ...) there are two possibilities:

Either the nail in A fixes the orientation of the spring, which sounds closest to what you initially describe. Than it will simply mediate torque from your system to what ever it is pinned to, resolving your overall angular momentum conservation.

Or the whole spiral plus mass may rotate ideally around that nail such that no angular momentum may be passed on. But then your spring, beeing mass less, will absorb all force in the tangential direction (still no mass, no angular momentum) and the massive bead will move radially inwards (also without angular momentum). (This is the idealized limit of the more real life situation with finite mass of the spring as explained by Floris.)

Answer 4

Angular momentum is only conserved in systems that have rotational symmetry. Assuming a fixed loop, if you consider as your system the bead and the spring, it is not symmetrical, and therefore, the angular momentum is not conserved. But if you consider the whole universe as your system (and, for a simplified universe, we consider the bead, the spring, the loop, and the Earth), you do have symmetry: if you rotate the Earth, the system is the same. So, when you release the marble, it will rotate one way, and the Earth will rotate so slightly the other way.

If you still have doubts, let me put a simplified example with linear momentum. If you have a ball on top of a tilted plane and let it go, it will gather momentum as it goes down (it is not conserved). But if your tilted plane is on wheels, you will see that it is pushed backwards: the total momentum (ball plus plane) is conserved.