2

Let foo be some unit of distance and bar be some unit of time which have been chosen so that the speed of light c = 1 foo/bar. Position several observers along a line each separated by one foo, and place light sources some distance apart amongst the observers, initially off. All observers and light sources are stationary with respect to one another.

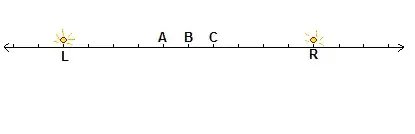
diagram

So in my diagram the tick marks are the observers, and the scale is one foo. For the example, the light sources are ten foo apart at points L and R.

Now at time 0 bars, ignite both light sources.

In the diagram, at time 4 bars, A has observed source L but not R, C has observed R but not L, and B has not yet observed either light source. At time 5 bars, B observes both light sources, and at time 6 bars all three labeled observers have observed both light sources. At time 7 bar, a total of five observes (A, B, C, and two unlabeled) have observed both sources.

Let r be the length of the line segment containing all observers that have observed both light sources. In other words, r is the length of the intersection of the event horizons on the two ignition events (I think I am using that term right, if not, please let me know). It seems that dr/dt = 2 foo/bar; for instance, in the 1 bar interval from 6 to 7, the change in r was 2 foo. As c = 1 foo/ bar, r is growing at twice the speed of light.

Since r is not a particle and cannot be used to transmit information amongst the observers, is there any contradiction here? Have I made any logical falicies?

David Z
  • 77,804
cobaltduck
  • 523

2 Answers2

6

The theory of relativity is often expressed as "Nothing can be faster than the speed of light". This is wrong.

You can always define certain things that seem to "move" faster than the speed of light. For example, if you shine a laser pointer at the moon and wiggle it around, the little red dot on the moon's surface can "move" faster than the speed of light.

A better way to express that the speed of light poses a certain limit is to say that two space-time events $(x_1, y_1, z_1, t_1)$ and $(x_2, y_2, z_2, t_2)$ can only be in a causal relationship if the distance of the space-points is so low that light can move from one to the other in time at most $t_2 - t_1$.

The distance between two events in space-time is defined as $$c^2 (t_1 - t_2)^2 - (x_1 - x_2)^2 - (y_1 - y_2)^2 - (z_1 - z_2)^2 - $$. Distances can be space-like and time-like, with space-like distances being those where the distance above is negative and time-like distances being those where the distance above is positive.

If it is positive, this means that the time-difference $t_1 - t_2$ is enough for the light to move from $(x_1, y_1, z_1)$ to $(x_2, y_2, z_2)$, and if it's negative, then, well, light cannot move from one point to the other point in time $t_1 - t_2$.

The right way to express that "nothing" can be faster than the speed of light is to say that two space-time events $e_1$ and $e_2$ can only be in a causal relationship if their distance is time-like.

Thus, your paradox vanishes if you realize that the growth of $r$ is related to two events that are not in a causal relationship because their distance is space-like.

Maybe this becomes easier to imagine if you think of a more extreme example: Think of $n$ light bulbs all a distance $\Delta$ apart, and each of them is connected to a timer. The timers are synchronized and programmed so that timer number $i$ turns the light bulb on at time $i * dt$.

So what you'll see is that lightbulb $i$ is turned on at time $i * dt$. The location of the last switched on light-bulb therefore "moves" with speed $\Delta / dt$. If you make $\Delta$ large enough and $dt$ small enough, this speed will be faster than the speed of light. But the way we have constructed this chain of bulbs already tells you that the switching on of the light-bulbs is not related causally, since they all have their own chip switching them on. Puh, I hope this makes sense :)

Lagerbaer
  • 15,136
  • 4
  • 77
  • 83
3

Lagerbaer gives an excellent detailed explanation, but to put it more simply: there is no contradiction, no logical fallacy, the distance $r(t)$ as you have defined it does indeed grow at a rate of $2c$ as measured by any of the observers A, B, C, etc. But $r$ does not correspond to a real thing. It does not measure the position of a particle or an information signal relative to that of an observer, so there's no reason it can't grow faster than light.

David Z
  • 77,804