Intuitive meaning of Dot Product

Question

I know intuitively that the Cross Product of two vectors $\vec{A}$ and $\vec{B}$ represents another vector $\vec{A \times B}$ perpendicular to it. In study of physics we come across this situation a lot. Hence I can visualize some applications of it

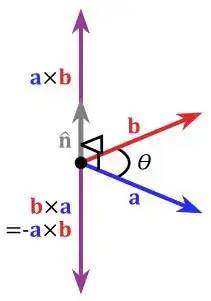
I know that the dot product of two vectors $\vec{A}$ and $\vec{B}$ is scalar quantity and also that it represents angular relationship between $\vec{A}$ and $\vec{B}$ .i.e.

• If $\vec{A}$.$\vec{B} = 0$. Then $\vec{A}$ and $\vec{B}$ are perpendicular.
• If $\vec{A}$.$\vec{B} > 0$ (Positive). Then the angle between $\vec{A}$ and $\vec{B}$ are less than $90^o$.
• If $\vec{A}$.$\vec{B} < 0$ (Negative). Then the angle between $\vec{A}$ and $\vec{B}$ are greater than $90^o$.

But I won't be able to understand intuitively, What does the dot product represents. What does the magnitude of the dot product of two vectors represents.

Answer 1

The product may be understood geometrically as the projection of one vector onto another, multiplied by the length of the vector that it is projected onto. If one takes the dot product of two vectors $\vec{a}$ and $\vec{b}$, we can apply this procedure to find the correct formula for the dot product:

Let's call the angle between the vectors $\varphi$. Then, the projection of $\vec{a}$ onto $\vec{b}$ is $|\vec{a}|\cos \varphi$. Multiplying by the length of $\vec{b}$ gives us $$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\varphi$$ This is the correct expression for the dot product. Of course, the dot product is symmetric so we might as well picture it as projecting $\vec{b}$ along $\vec{a}$.