How loud is the thermal motion of air molecules?

Question

In other words, given a magical room with walls that produce no vibration and transmit zero vibration from the outside, and nothing on the inside except room temperature air, what would be the noise level in dB SPL (sound pressure level) from the thermal motion of the air itself? (Similar to the noise floor of electronics being determined by thermal noise in the conductors.) What is the quietest possible anechoic chamber? What is the noise floor of air?

For reference: Sound pressure is defined as the root-mean-square value of the instantaneous pressure, measured in pascal = N/m². SPL is the same number, but expressed in decibels relative to 20 µPa.

(I assume that it has a white spectrum, but I could be wrong. Thermal noise in electronics is white, but other types of electronic noise are pink, and blackbody thermal radiation has a bandpass spectrum.)

Here's an explanation in the context of underwater acoustics. Not sure how this applies to air:

Mellen (1952) developed a theoretical model for thermal noise based on classical statistical mechanics, reasoning that the average energy per degree of freedom is kT (where k is Boltzmann’s constant and T is absolute temperature). The number of degrees of freedom is equal to the number of compressional modes, yielding an expression for the plane-wave pressure owing to thermal noise in water. For non-directional hydrophones and typical ocean temperatures, the background level due to thermal noise is given by:

NL = −15 + 20 log f (in dB re 1 µPa)

where f is given in kHz with f >> 1, and NL is the noise level in a 1 Hz band. Note that thermal noise increases at the rate of 20 dB decade⁻¹. There are few measurements in the high-frequency band to suggest deviations from the predicted levels.

Citation is R. H. Mellen, The Thermal-Noise Limit in the Detection of Underwater Acoustic Signals, J. Acoust. Soc. Am. 24, 478-480 (1952).

Answer 1

Apparently the search term I was missing was "Brownian motion". With that, I found several leads. They contradict each other somewhat, but I can at least post a partial answer:

Geisler - Sound to Synapse: Physiology of the Mammalian Ear:

Estimates for the first of these sources, the pressure fluctuations due to the Brownian motion of air molecules impinging on the eardrum, are about 2 µPa (−20 dB SPL), when the frequency bandwidth relevant for the detection of a 3 kHz tone is included (Harris. 1968). Calculations using this number suggest that the behavioral thresholds of humans for 3 kHz tones are not limited by this Brownian motion, but that those for the most sensitive of cats may approach it (Green. 1976)

Dallos - The Auditory Periphery Biophysics and Physiology:

By assuming a 1000-Hz bandwidth, Harris computed that the Brownian motion of air molecules generates a mean pressure fluctuation of 1.27×10⁻⁵ dyne/cm² [−24 dB SPL]. The usually accepted value of sound pressure corresponding to free-field listening threshold is 18 dB above the pressure level of thermal fluctuations. Thus one can immediately see that Brownian motion of air molecules is certainly not the limiting factor of our hearing sensitivity.

There's another available with more details:

Harris - Brownian motion and the threshold of hearing:

We can avoid the calculation of the Brownian noise at the eardrum by using the Brownian noise in a free field and comparing that with the minimum audible field (MAF) instead of the minimal audible pressure (MAP).

If we use frequency limits of 2500 Hz and 3500 Hz. we obtain a root mean square (rms) pressure fluctuation of 98 db below 1 dyne/cm² [−24 dB SPL]. The MAF² is about 80 db below 1 dyne/cm² at 3000 Hz. This is 18 db above the estimate of Brownian noise. It seems clear from this calculation that Brownian noise in the air is not a limiting factor to the threshold of hearing.

2.5 kHz to 3.5 kHz is not the total bandwidth that would be picked up by a microphone, though.

Yost & Killian - Hearing Thresholds:

By making some assumptions about the acoustic energy present in the Brownian motion of air molecules, it can be shown that a sound presented at 0 dB SPL is only 20-30 dB more intense than that being produced by Brownian motion

So −20 to −30 dB SPL.

Howard & Angus - Acoustics and Psychoacoustics:

At 4kHz, which is about the frequency of the sensitivity peak, the pressure amplitude variations caused by the Brownian motion of air molecules, at room temperature and over a critical bandwidth, correspond to a sound pressure level of about −23 dB. Thus the human hearing system is close to the theoretical physical limits of sensitivity. In other words there would be little point in being much more sensitive to sound, as all we would hear would be a ”hiss” due to the thermal agitation of the air!

I would still like to know:

• How this is derived
• What the spectrum is, and if it's different from the violet spectrum in water, why?
• What the 20 Hz-to-20 kHz and A-weighted values are

Update

I believe I've found an answer in these two papers, though both have errors that make it difficult to be sure:

• Harris, G. G. Brownian motion in the cochlear partition. J Acoust. Soc. Am. 44: 176-186, 1968
• L. J. Sivian and S. D. White, On minimum audible sound fields. Journal of the Acoustical Society of America, 1933, 4, 288-321

Harris's equation 1 is taken from Sivian-White, but seems erroneous. The original is dimensionally consistent, at least:

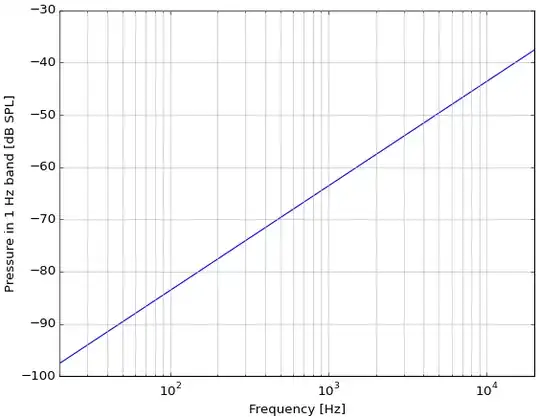
$$\overline P = \left [ \int^{f_2}_{f_1}{P_f}^2\cdot df \right ]^{1/2} = \left [ \frac{8 \pi \rho k T} {3c} ({f_2}^3-{f_1}^3)\right ]^{1/2}$$

where $\overline P$ is RMS pressure, $\rho$ is density of air, $k$ is Boltzmann's constant, $T$ is temperature, $c$ is speed of sound, and $f_1$ and $f_2$ are the bandwidth limits.

Sivian-White then calculate $5\times 10^{-5}$ bars for 1000–6000 Hz, which... also seems erroneous. That's equal to 5 Pa, or 108 dB SPL? If I calculate over the same range, I get 5.3×10⁻¹¹ bars = 5.3 µPa = −11.6 dB SPL, which seems more reasonable.

Now Harris says:

Also, a more accurate estimate of the Brownian noise would take into account the properties of a semi-rigid eardrum in an ear canal and not treat the tympanic membrane as an infinite reflecting wall. We can avoid this type of calculation by using the Brownian noise in a free field and comparing that with the minimum audible field (MAF) instead of the minimum audible pressure (MAP). The free-field Brownian motion is 3 dB less than that given by Eq. 1 owing to the fact that the waves traveling in opposite directions are not correlated in a free field, but are at a reflecting wall

When I use Sivian's equation and Harris' −3 dB with Harris' frequency band of 2500–3500 Hz, I get Harris' answer of 1.273×10⁻⁵ dyne/cm² (= 1.27 μPa = −24 dB SPL) so it seems like I'm doing it right.

But they're interested only in whether the self-noise of air is close to the threshold of hearing in the most sensitive band. Calculating total SPL, in the same way but over 20 Hz to 20 kHz, I get 21.8 μPa, very close to 0 dB SPL. Coincidence?

This equation also lets us calculate the spectral density, which seems to be violet noise, increasing by 6 dB every octave, same as the underwater reference in the question:

Answer 2

I think this is indeed a very interesting question. When I first read the answer by endolith I thought that it was not right, because it is based on a very simple Rayleigh-Jeans estimate that goes back to a paper from 1933, published long before Landau and Lifshitz developed the modern theory of fluctuations in fluid dynamics (1957, described in vol II of the text book on Statistical Physics). However, upon further reflection I do think that it is indeed a reasonable estimate for sound waves in the audible range.

The general formula for pressure fluctuations in a fluid is worked out in the text book by Landau and Lifshitz (LL) mentioned above. It is based on the linearized Navier-Stokes equation augmented by noise terms, where the strength of the white noise is fixed by fluctuation-dissipation relations. The resulting pressure fluctuations are $$ \langle \delta P\delta P\rangle_{\omega k} = 2 \,{Re}\, \frac{k^2\rho T u^4(i+\gamma_T\omega/(uk^2))} {\omega(\omega^2-k^2u^2)+2i\omega u\gamma}. $$ Here $\langle\delta P\delta P\rangle_{\omega k}$ is the pressure correlator in Fourier space, $Re$ denotes the real part, $u$ is the speed of sound, and $\gamma$ is the sound attenuation rate $$ \gamma = \frac{k^2}{2\rho u}\left[\zeta +\frac{4}{3}\eta +\frac{\chi u^2\rho^2}{T} \left(\frac{\partial P}{\partial T}\right)_s^2\right], $$ where $(\zeta,\eta,\chi)$ are the bulk viscosity, shear viscosity, and thermal conductivity. Also, $\gamma_T$ is the thermal conductivity part of $\gamma$.

This is more complicated than the Rayleigh-Jeans formula, but the general structure follows from the nature of the excitations in a fluid. In particular, in fluid dynamics we have propagating sound modes with $\omega^2=u^2k^2$, and diffusive propagation of heat, $w=i\chi k^2$. I can integrate over $k$ in order to determine the frequency power spectrum. This is complicated in general, and requires a UV cutoff, or some knowledge of experimental resolution. Here, we can make use of the fact that audible sound is not strongly attenuated. Including only the sound peaks, and performing the integral based on a Lorentzian approximation to the line shape, gives $$ \int d^3k \, \langle \delta P\delta P\rangle_{\omega k} = \frac{8\pi^2\rho T\omega^2}{u} $$ which looks (up to a factor 1/3?) like the formula in the Rayleigh-Jeans limit.

So why is this not white or Brownian noise? The source term is indeed white noise, but the power spectrum is determined by the eigenmodes of the Navier-Stokes equation, which are more complicated than just a Brownian particle (in particular, there is a continuous spectrum, labeled by $k$). Also note that we have ignored the diffusive part of the power spectrum, so this result is only valid in some range of $(\omega,k)$.