Why does gravitational collapse occur suddenly in a supernova progenitor?

Question

I was reading the Wikipedia article on Supernovae, and it says that one of the reasons why a supernova occurs is due to sudden gravitational collapse when the core of the star has little fusable material. But why is this collapse sudden? Shouldnt the collapse be gradual as the fusable material gradually decreases? Why is the sudden collapse like driving off a cliff? (if I've interpreted the article rightly.)

Answer 1

Star are fighting against gravitational forces by pressure gradients due to fusion in the core (and the shells outwards). Once fusion stops, there is no pressure gradient and gravity wins the "battle."

The classic picture of a massive star at the end of its life is (and obviously not to scale),

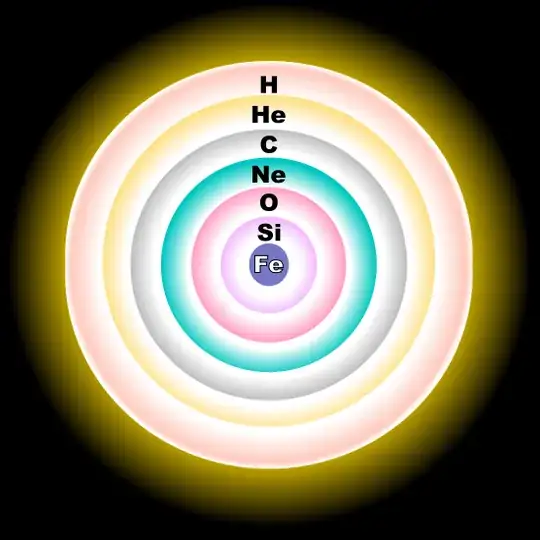
But each star star started off with just hydrogen in the core. Through the pp-chain, it produced helium in the core, and so on down the line until iron is produced in the core. Iron has the most nuclear binding energy of all elements, so once you make it you, can't really make anything else via fusion.

The duration of each burning phase is well known (depends on mass of star, but the following values can give a good estimation of why the collapse is so sudden; the case presented is the core-burning timescales for a 15 solar mass star): $$ \begin{array}{ccc} \textbf{Burning} & \textbf{timescale}&\textbf{core density}\\ {\rm H} & \sim10^{7}\,{\rm yrs}& \sim6\,{\rm g/cm^3}\\ {\rm He} & \sim10^6\,{\rm yrs} &\sim10^3\,{\rm g/cm^3}\\ {\rm C} & \sim10^3\,{\rm yrs} &\sim10^5\,{\rm g/cm^3}\\ {\rm Ne} & \sim1\,{\rm yr}& \sim10^7\,{\rm g/cm^3}\\ {\rm O} & \sim2\,{\rm yrs}& \sim10^7\,{\rm g/cm^3}\\ {\rm Si} & \sim20\,{\rm days}& \sim10^7\,{\rm g/cm^3}\\ {\rm Fe\,\,burning} & \sim1\,{\rm sec}&\sim10^9\,{\rm g/cm^3} \end{array} $$

So the collapse timescale of a $\sim1.5\,M_\odot$ core of iron-group elements takes less than one second: $$ \tau_{collapse}\simeq\frac{1}{\sqrt{G\rho}}=\frac1{\sqrt{6.67\times10^{-8}\cdot10^9}}\simeq0.12\,{\rm sec} $$ The core falls inwards at roughly $0.25c$, collapsing into a Neutron star in the process--the repulsive nuclear force and neutron degeneracy pressure are what halts the collapse when the density reaches nuclear densities of $\sim10^{14}\,{\rm g/cm^3}$. Again, due to the lack of a pressure gradient, the outer shells follow suit and collapse inwards.

Answer 2

An old, massive star near its death reaches the point of "burning" (this is nuclear fusion, not literal setting ablaze!) Si and O to Fe, which requires massive amount of energy for further fusion, therefore the fusion chain ends here temporarily. Fe "ashes" around the core fall inside, which further increase the core's mass up to the Chandrasekhar or Oppenheimer-Volkoff limits. This increases the core's temperature, therefore photons become so energetic as to make Fe split into α particles and protons (photodisintegration), which reduces the core's mass and the pressure, because this reaction is very endothermic. Also, inverse β decay leads to further decrease in pressure, which reaches the point that hydrostatic equilibrium ceases, hence the star collapses in free-fall time-scale, which is independent of the distance, it only varies as $\propto \rho^{-1/2}$. This implies that outer layers of the core collapse faster than the inner ones. To see how fast this process is, if the Sun would become supernova (impossible, it is too small), the free-fall time-scale would be of order of an hour. As the outer layers fall, they reach supersonic speed and become completely separated from the rest of the star. The core reaches nuclear density, therefore the collapse stops there, but it creates a shockwave that traverses the core and decomposes Fe, a process that is extremely energy consuming. This is the supernova explosion.

Answer 3

The core-collapse phase of a supernova commences once the final stages of nuclear burning are complete. This final phase of fusion reactions involving silicon, produce a core composed of iron-peak elements (not just iron). The cessation of nuclear burning leads to the contraction of the core. This happens relatively slowly at first, on a timescale given by the core thermal energy divided by its neutrino luminosity; the core is still supported by relativistic electron degeneracy pressure, which is almost independent of temperature. ie. The end of nuclear burning does not in itself trigger the rapid core collapse, but the core is very close to or beyond the Chandrasekhar limit, with an equation of state that has an adiabatic index $\sim 4/3$, and hence is on the cusp of instability.

The really rapid collapse is initiated either by photodisintegration (in more massive progenitors) or electron capture in the more common 10-20$M_{\odot}$ progenitors.

Rapid core collapse can be started if the core, of mass about 1.2-1.3$M_{\odot}$, becomes unstable to electron capture. This happens once the densities become so high that free, degenerate electrons at their Fermi energy, are sufficiently energetic to create neutrons in weak-interactions with protons. This initially happens inside nuclei, making them more neutron-rich. However, photo-disintegration processes will also break up some of the nuclei and release free protons. The electron threshold energy for the creation of neutrons from free protons is much lower, so many more electrons are capable of taking part in electron captures once this happens.

Electron capture is the equivalent of kicking away the star's support. Because electron degeneracy is so important for supporting the core, when free electrons are removed by electron capture, it is very difficult to increase the pressure as the core collapses (as I mentioned previously, any increase in temperature is almost irrelevant to the electron degeneracy pressure) and so the collapse accelerates until it proceeds essentially on the free-fall timescale of the core. Radiation pressure is not important and at this point the copiously produced neutrinos are able to escape freely.

In higher mass stars the core may be hotter and of slightly lower density. As temperatures reach about $10^{10}$K then iron-peak nuclei can be photodisintegrated into alpha particles and neutrons. These reactions require energy and it is taken out of the internal energy of the gas, drastically reducing the pressure and leading to nearly free-fall collapse.

For a 1.4$M_{\odot}$ core with a radius of 1000-2000km, the free-fall time is about $(G \rho)^{-1/2} \simeq 0.1-1.0$ seconds.

Although the core temperature and pressure do rise again during the collapse, the collapse cannot be arrested until the central density becomes high enough ($3\times10^{17}$ kg/m$^3$, at a radius of about 20km) for the equation of state to stiffen due to neutron degeneracy pressure and nucleon interactions.