When a star turns into a red giant what stops its core contracting

Question

I recently asked this question When do stars become red giants? and am now wondering when the star's core is contracting after it has fused $H$ to $He$ what force stops the contraction just before it becomes a red giant?

Answer 1

The answer depends upon the mass of the star.

For stars of less than 2 solar masses, electron degeneracy pressure stops the collapse.

For more massive stars, helium fusion begins which stops collapse, without a degenerate state being reached.

Answer 2

$$\frac{dP} {dr} = -\frac{GM\rho}{r^2} $$Where $P$, is electron degeneracy pressure, $ G $ is a constant, $M$ is the mass enclosed in a shell of radius $r$ with density $\rho$.

In short, electron degeneracy pressure ( left hand side ) generated by electron degeneracy is opposite and equal to gravity ( Right hand side ). Where electron degeneracy is a result of the Pauli Exclusion Principle. We have so many electrons in such a small volume, and of course per the exclusion principle, none of these can exist in the same quantum state. By trying to force these electrons into this smaller and smaller region, the laws of quantum mechanics fight back by resisting being in such a small volume, this generates the aforementioned electron degeneracy pressure. For more detail see here, where the analytic solution for the pressure part of the above Hydrostatic Equilibrium Equation is defined.

Answer 3

Nothing stops the core contraction until He ignition takes place!

Yes, the core is partly supported by electron degeneracy, this slows the contraction and allows a relatively stable period of shell H-burning, but the central density continues to rise and the core contracts until He is actually ignited. This is especially true where there is a high degree of degeneracy. The mass of the core increases as more He ash accumulates from the H-burning shell above; the core shrinks further because, for an object supported by a degenerate equation of state, the more massive it is, the smaller it has to be. It is the core contraction and relocation of the H-burning shell to hotter temperatures that causes the increase in luminosity characterizing the ascent of the giant branch.

In a lower mass star, the pressure builds up very rapidly until He is ignited in a runaway "flash", the degeneracy is lifted, and the core expands significantly (see diagram below). In higher mass stars ($>2M_{\odot}$), where the core was not very degenerate, the He is ignited more gradually and the core contraction is halted more gradually.

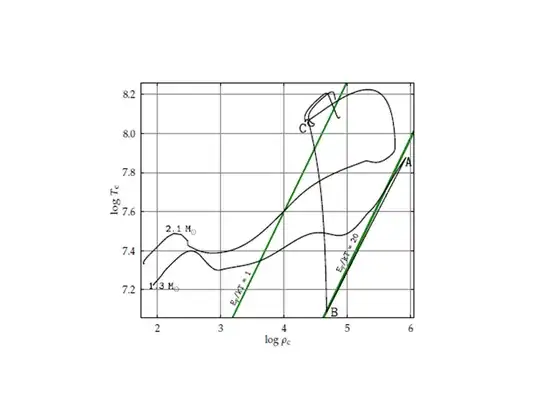
Here is a diagram of the central density vs central temperature for stars of 1.3 and 2.1$M_{\odot}$ leaving the main sequence and igniting He in their cores - at point A for the lower-mass star, which undergoes a helium flash. The main sequence is to the bottom-left of the diagram. The diagram is from a thesis by Gautschy (2012). The two green lines mark first (left) where partial degeneracy is felt in the core, then on the right (only reached by the lower mass stars) where a high level of degeneracy is reached.

Note that the central density monotonically increases from the main sequence until He is ignited (the star is already a red giant at this point).

Edit and postscript:

It can't be true that electron degeneracy halts the core contraction (except in stars with $M<0.5M_{\odot}$). If that were the case, the core could cool and yet still support the star and He burning would never take place - leading to the formation of a He white dwarf.