Reconciling total internal reflection and the evanescent Wave

Question

I understand that light is guided in a dielectric waveguide via total internal reflection. My question is regarding the origin of power contained in the evanescent field traveling along the direction of propagation.

From Fresnel equation we get that the reflection coefficient is %100 for angles above or equal to the critical angle as shown in the following figure:

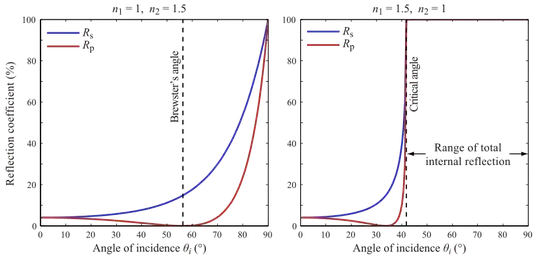
It is clear from the figure that no power is transmitted from medium 1 to medium 2.

However, from dielectric waveguide theory we know that some power is contained in medium 2 and we define the confinement factor which is a measure of amount of power confined in the core of the waveguide compared to the power contained in the evanescent field. The confinement factor is defined as following:

$$\Gamma = \dfrac{\int_{-L_x/2}^{L_x/2}| \mathcal{E}_x|^2dx}{\int_{-\infty}^{\infty}|\mathcal{E}_x|^2dx}$$
Therefore my question is how to reconcile the two facts that no power is transmitted into medium 2 and existence of power in medium 2 carried by the evanescent wave ?

Answer 1

It's a "tunneling" behavior. In effect, all the light is "pulled back" into the medium unless there's another body of high-index (well higher than the $n_1 = 1$ ) material within the distance covered by the evanescent wave. If that material is close enough, then that part of the evanescent wave, which you can view as a probability wave, is in a region where the light itself can again manifest (because $n_1 and n_3 $ are such that total internal reflection between these two materials will not happen at the existing incidence angle).

So, no power is transmitted by medium 2, but the wave function is still nonzero there.

The same mathematics which govern electrons tunneling out of quantum wells works just as well here, BTW

edit :

I should have written that no power is transmitted perpendicular to the interface. As several comments point out, energy can be carried parallel to the interface in medium 2, as happens in the cladding of optical fibers.