How can current be a smooth curve?

Question

The following is a graph of the current across some circuit element:

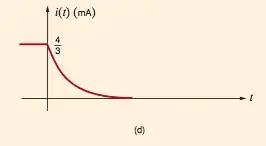
Note how the current is treated like a smooth continuous function. Even in the analysis of things (i.e. analysis of the transient state of an RC circuit) current is treated like a continuous smooth function.

This is how currents works:

Say you have a voltage source connected to some wire which is then connected to some component. A field will be established in the wire, and electrons will move around for say $t$ seconds, creating surface charge to ensure the field is uniform and points in the correct direction. The period during which surface charge moves around to establish the field is known as the transient state. For a more detailed explanation, see: https://physics.stackexchange.com/a/102936/28118

This transient state lasts for a very short time - a couple of nanoseconds, but exists none the less. So there is a short time between when the voltage source is connected and a current is established.

Now say the voltage source is non-constant. Say it starts of at a voltage V when you connect it to a circuit. The transient state will exist for a couple of nanoseconds and then current will be established. Now say you increase the voltage. The transient state will happen again and then a new current will be established.

My point is that the current doesn't change "smoothly". Rather, it's a bunch of discrete points, with the space between the points being the transient state and therefore having an undefined current.

Q1) So why is it valid to treat current like a continuous function instead of the discrete function that it is?

Q2) Say you have a current pulse function:

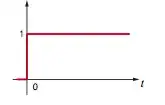
In real life, would the function really be a pulse or would it really be an extremely steep line (but a slope of non-infinity none the less)? I would expect the slope to be non-infinity since it would take a couple of nanoseconds to establish the current instead of it being immediate as the function suggests.

Answer 1

If you want to include "all real world effects" in your analysis, you need to make sure you include all effects. At the very least, include parasitics. And include the fact that your "real world voltage source" has finite impedance, output capacitance, inductance in the leads, ...

So when you state

Say it starts of at a voltage V when you connect it to a circuit. The transient state will exist for a couple of nanoseconds and then current will be established. Now say you increase the voltage. The transient state will happen again and then a new current will be established.

you are ignoring many things. Things that matter.

Let's assume I have a voltage source with an output impedance R and capacitance C, and I connect it to another circuit (from your diagram I am guessing there's an RC in there) with a lead that has inductance L.

When the connection is made (actually, just before the connection is made) electrons at the circuit end will notice the electric field from the wire that is approaching (which is at a different potential) and will be attracted (assuming a positive voltage source). The current that starts to flow is limited by the inductance of the wires - while it is small, it represents significant impedance when the rate of change of current is large.

Since $$V=-L\frac{dI}{dt}$$

a step change in voltage will lead to at most a ramp in the current, not an infinitely steep jump - so you will for sure have a valid first derivative.

As for your second question - yes, any "step" is in reality a (short) ramp. This is something that becomes particularly important in high speed communications, where the "digital" signals (binary actually) start to look more and more like analog signals, and less like 0s and 1s. The same is true in computers - at the current clock speeds, you need to worry about parasitics, termination, rise times... the world of digital electronics is, in the final analysis, still analog.

There are entire fields of study devoted to making really, really fast signals - I believe the current world record is held by Northrop Grumman who have a 670 GHz circuit. That is crazy fast - but still a finite time. To get there you need to make things super small - to get rid of the parasitics. For the rest of us, getting rise times below a few 100 ps is surprisingly difficult.

So "continuous" is really just a matter of "how hard you look". And when you go down to the level of individual electrons, all this breaks down further. If you detect individual electrons arriving you are back in the discontinuous mode.

Ultimately, you need to approach this (and any) problem with a practical stance: how detailed does my model need to be in order to be able to predict behavior that I care about? That is the level of detail you need to include - everything else is a distraction.