A uniform rod$(m,l)$ is standing vertically on a horizontal frictionless surface. Gravity is downwards and uniform. I give its upper end a little push and off it goes. I want to find the Normal Force(and all other variables) as a function of time.
Here's what I do :
$mg-N=ma$
Where a is downward acceleration(and the only) of centre of mass wrt ground.
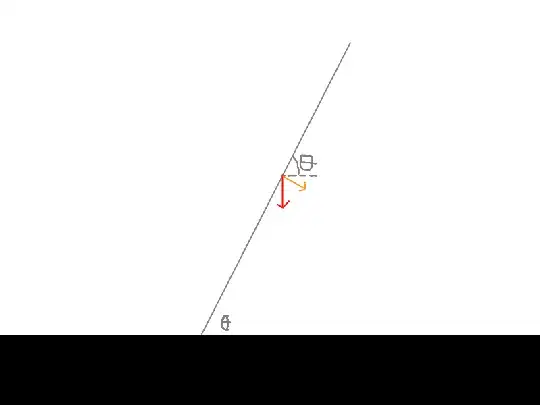
Next, I think of conservation of energy. I assume it rotates $\theta$ from vertical
$mg\frac{l}{2}(1-\cos\theta)=K.E.$
I have problem writing expression of its Kinetic Energy. I have studied about instantaneous centre of rotation.
So, I can write its speed and rotational kinetic energy about it as $K.E.$? Also How do I find relation between $\omega$ (angular velocity about that instantaneous centre) and velocity of rod?