We don't normally answer homework question in full, but I'll answer because I'm very eager to make the point that the best, by far, method of answering questions like this is to choose relevant spacetime points in $S$, apply the Lorentz transformations and find where the points are in $S'$. This normally makes the answer obvious.
In this case we have a pair of photons travelling along in $S$ with a distance of $\ell$ between them. Let's choose our $x$ axis so that the photons are travelling along it, and we'll choose the origin so that in $S$ the rear photon is at the point $(t = 0, x = 0)$. This means that at time zero the front photon is at $(0, \ell)$:
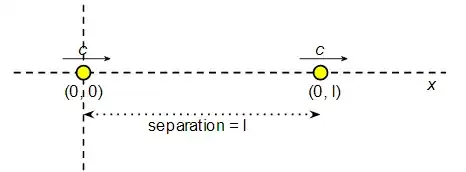
All we have to do is find the two points in $S'$, and work out the spacing between them and we'll have our answer. The Lorentz transformations are:
$$ t' = \gamma (t - \frac{vx}{c^2}) $$
$$ x' = \gamma (x - vt) $$
If we feed in the first point $(t = 0, x = 0)$ we just get $(0, 0)$, so in $S'$ the rear photon is at the origin. If we feed in the position of the front photon $(0, \ell)$ we get:
$$ t' = \gamma (t - \frac{vx}{c^2}) = -\gamma\frac{v\ell}{c^2} $$
$$ x' = \gamma (x - vt) = \gamma\ell $$
So in $S'$ the front photon is at $(-\gamma\frac{v\ell}{c^2}, \gamma\ell)$. But we don't want to know the position of the front photon at time $t' = -\gamma\frac{v\ell}{c^2}$, we want to know it at time $t' = 0$. So we wait a time $-\gamma\frac{v\ell}{c^2}$ during which the photon (travelling at $c$) moves a distance $c\gamma\frac{v\ell}{c^2} = \gamma\frac{v\ell}{c}$. So at time zero in $S'$ the position of the front photon is:
$$ \left(0, \gamma\ell + \gamma\frac{v\ell}{c}\right) $$
and the spatial separation between the two points is just the $x'$ coordinate of the front photon:
$$ \ell' = \gamma\ell + \gamma\frac{v\ell}{c} \tag{1} $$
The rest is just algebra. The question defines $\beta = \frac{v}{c}$, and the Lorentz factor $\gamma$ is then given by:
$$ \gamma = \frac{1}{\sqrt{1 - \beta^2}} $$
Substitute this into equation (1) and we get:
$$\begin{align}
\ell' &= \ell\left( \frac{1 + \beta}{\sqrt{1 - \beta^2}} \right) \\
&= \ell\left( \frac{1 + \beta}{\sqrt{(1 - \beta)(1 + \beta)}} \right) \\
&= \ell\left( \frac{\sqrt{1 + \beta}}{\sqrt{1 - \beta}} \right) \\
&= \ell\left( \frac{1 + \beta}{1 - \beta}\right)^{\tfrac{1}{2}}
\end{align}$$
Which is what we were asked to prove.
