Why does a cup with 100 g water float when placed on another cup with 50 g of water?

Question

Imagine we have cup A with 50 g of water and cup B (smaller in width than A) with 100 g of water. Now put cup B into cup A. If the width of both cups are of comparable size then the cup with 100 g of water floats. It does not touch the bottom of cup B.

Now think about Archimedes law of flotation. It says that the weight of displaced liquid = weight of the floating object. However in this case the bottom cup has only 50 g of water. How can an object float without displacing water equal to its own weight? Am I not applying Archimedes principle correctly or because of both things beings of comparable size Archimedes principle does not apply?

Answer 1

As best I can tell, what you're confused about is the fact that Cup A (weighing 100 g) is floating in 50 g of water, while Archimedes principle states that Cup A ought to be displacing 100 g of water, which seems to contradict the fact that there's only 50 g of water available to displace. How can that be possible?

There is a subtle reason; just because you have 50 g of water doesn't mean you can't effectively displace more than 50 g of water. This is probably best illustrated with a picture. Here's what the system looks like before Cup B is dropped in:

Here's what it looks like when you drop in Cup B:

The tricky thing is: Cup B effectively displaced 100 g of water, even though there was only 50 g of water available to displace! If it's not immediately obvious how it is that Cup B is displacing 100 g of Cup A's water (even though Cup A only has 50 g of water), stare at diagram 2 for a while.

Answer 2

Let's assume that cup B has a mass of 1 g, so the total mass it needs to displace for it to float is 101 g. When cup B is placed in cup A, the level of the water rises. With cup B floating, we mark the level of the water in cup A. We take out cup B and notice the level of water is lower. If we now add water to cup A to bring it up to the earlier level, we would need to add 101 g of water.

Answer 3

Depth is what matters here.

1. It is a given that a partially filled cup will float in a body of water. Of course, that body just has to have enough depth to contain the immersion. If the cup requires X centimeters of depth in order to float, and the surface of the water is > X centimeters above the bottom of the larger container (taking into account the displacement caused by the immersion), then the cup will float.

2. The depth of the water is not restricted by the available volume. 50 grams of water can be displaced in such a way that sufficient depth is created to float a cup of 100 grams.

Depth, together with density and gravity is what actually creates the pressure that causes buyoancy. Each unit of area of the object is acted upon by pressure, and the net difference in pressure between the upper and lower parts of the object creates buyoancy: because the parts of the object's surface which are deeper are subjected to greater pressure than the parts of the object's surface which are immersed less deeply.

Archimedes' Law is just a corollary which arises from this pressure gradient. Because of the way the surface integral works out around an object, a short-cut pops out from the mathematics: the buoyant force can be obtained knowing just the gravitational force which acts upon the equivalent volume of the fluid in which the object floats. This is usually stated as "the volume displaced by the object", but the displacement is an abstraction: there might not be enough fluid available such that when the buoyant object is removed, its entire volume is filled by the fluid that remains.

The "displacement visualization" of buyoancy assumes that the body of water is large enough that the availability of fluid is practically unlimited. But buyoancy does not depend on actually pushing out all the fluid out of the object's space; it's just that: a visual aid.

This is all related to the fact that the pressure in a column of fluid under gravity is irrespective of the width of that column and therefore its volume. A column of water 10m high, and as thin as a pencil, has the same pressure at the bottom as a 10m deep lake (aobut 1 atmosphere). This is why only a thin jacket of water around a paper cup is enough to create the pressure to float that cup.

Answer 4

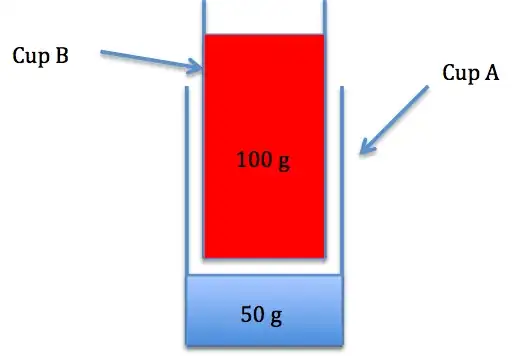
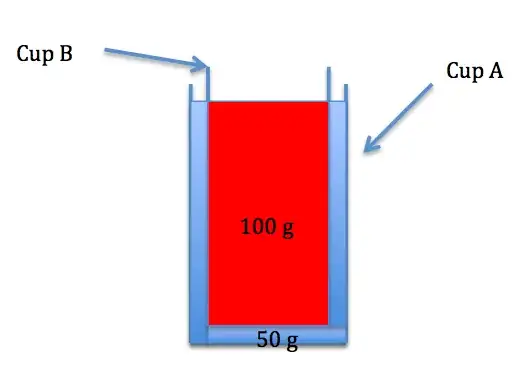
How about this experiment:

Cup A is full of water to the rim. You place cup B filled with some water to float in cup A. Most of the water of cup A spills over the rim except for a tiny amount. However cup B finally floats in cup A. You pull the floating cup B out of cup A.

• How much water spilled from cup A?
• How much volume of water was spilled?
• Will cup B float again, if you put it back?

Bonus questions:

• By how much rises the water level, if you put a stone (smaller but as heavy as cup B) into cup A?
• Why doesn't the stone float?
• How much water do you need to fill into a cup C to make cup B float in it, if cup C equals cup A except for a higher rim?
• How much (more) volume of water would you need to fill into cup D to make cup B float in it, if cup D would be wider than cup A?

I guess the confusion arises from measuring water by its weight instead of its volume. The water spilled from cup A is the volume of water displaced by cup B. But you don't need to actually spill it. It's just important that the water level rises as much as if it was spilled.

And now to answer your question: You are applying the term "displace" incorrectly, because you relate it to the water that is still there. But the meaning is that it is not there, e.g. the spilled water. However spilling water is only a way to visualize that something is not there.

In short: Displacement does not mean "spilling", but raising the water level because a certain "volume is pushed aside".

BTW: The last paragraph in the marked answer is kind of critical:

The tricky thing is: Cup B effectively displaced 100 g of water, even though there was only 50 g of water available to displace!

The last verb shouldn't be "displace" but "push aside", otherwise it's the same erroneous way of thinking.