Let's suppose a pedestrian P is walking or standing next to a highway.
Suppose a truck T will drive by the said pedestrian at speed V leaving distance L between the two.
Assuming L is a reasonably small finite size how would one calculate the force acting upon the pedestrian from both the general differences in pressure and turbulence?
Shortly put, how fast would the truck have to go in practice so that the air flow left in its wake would pull the pedestrian onto the road?
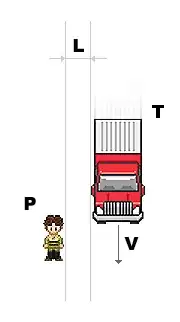
The truck will have in its wake some unknown mass of air almost moving with a speed $v$ comparable to the truck's speed $\bf V$. The pressure behind the truck will be lower than the pressure at the sidewalk because air pressure follows the Bernoulli equation, $$ P_\mathbf{P} = P_\text{road} + \frac{1}{2}\rho v^2, $$ where $\rho \approx 1~$kg/m$^3$ is the air density. For a truck at 60 mph $\approx$ 30 m/s, this is a pressure difference of 450 Pa, or 0.004 atm.
If the pedestrian is very near the wake of the truck (note that this wake will extend partway into the buffer zone $\bf L$), they might feel this pressure difference $\rho v^2/2$ across their torso. The force depends on the orientation and area of the pedestrian. My torso is about a meter long and about 0.4 meter wide, so I could feel a force as large as 180 N. That's equivalent to about 20% of my body weight, or the lateral force that I'd feel leaning at an angle of about 10º. I can recover from a 10º lean, but I have to be ready for it.
All of these numbers should be taken as coarse approximations, because I've ignored turbulence. Turbulence will play a huge role in the dynamics here, especially for finite $\bf L$. However the order of magnitude is probably correct.
