When I stretch a rubber band, it breaks. When I hold the broken ends together, why doesn't it join again?

Question

The question is simple. When we join the two broken surfaces, what is it that keeps the surfaces from connecting with each other, while earlier they were attached to each other? Also, would the two sides join again if I hold them together for an infinite amount of time?

Answer 1

You are thinking of a lego or a jigsaw puzzle. You have to think of huge numbers and tiny dimensions . There are $10^{23}$ molecules in a mole. The atomic dimensions are less than $10^{-9}$ meters. The lattice that has been broken will not fit the puzzle if it has been moved further than this last small distance because the molecular forces will not match. In addition the break will have displaced the locations of atoms and molecules on the two sides, in this microscopic distance making fusion even more improbable.

Answer 2

First of all you need to understand how the rubber is held together in the first place. Rubber, plastics, carbon fibre and pretty much all forms of living tissue are held together in the same manner. All, or a large part of the molecules are long strings, either repeating the same simple pattern, or a number of slightly different patterns organised in random order. In some cases the strings are several thousand atoms in length. When the strings are packed tightly together they attract one another, thus they end up sticking together, and because of the interlaced structure the combined strength is much larger than this attraction between two flat surfaces would be.

If you pull hard enough to break such a structure one or a combination of two things will happen:

1. The molecules slip out of their interlocked configuration, this leaves holes in both halves of the object where the molecules now belonging to the other half used to be, there is vacuum in these holes so they collapse almost instantly, all the lose threads of the broken ends fall towards the object and the majority of those surfaces where the two halfs were attracted end up attracting surfaces from the same half. Thus there is no room for the connections that used to be to be reformed. If you stick the two ends back together you can only hope to form a connection along the break surface, which will be much weaker as it lacks the interleaving, and even this is often impossible as air between the two objects prevent them from joining.

2. The molecules break. When you break a molecule through sheer force the resulting two molecules will typically be radicals. These radicals will react rapidly with other molecules, especially other radicals, so the broken ends will typically end up either binding to one another, or snatching some atoms from the air in order to patch the hole and stop being radicals. In either case this leaves the broken ends in a state where they will not simply rebond with their old counterpart.

Rubber in particular is a material that takes long to settle, the molecules of a common rubber band are slowly shifting positions, making and breaking bonds between molecules. This means that it is actually possible for some rubber bands to rejoin given time (or become a big clump in the pack), pressure or heat may speed up the process. Unfortunately this shifting also in general makes the rubber weaker with time, if it has shifted enough to rejoin it has probably also shifted enough to be uselessly weak.

Answer 3

Your question is perfectly valid despite most people may think it's odd as reason looks obvious.

There's a property of system called entropy which must not decrease for any process (do some research on web; You may have problem in understanding it as you're in high school). Only those processes in the universe happen in which entropy of system either stays same or increases. For all real-world processes, entropy increases (stays same thing is for ideal reversible processes).

When you touch something hot, heat is transferred from that object to your body. You can argue about that: "Why not opposite?" Your argument would be valid as energy conservation law wouldn't be violated even if heat transfers from your body to that hot object. You can do such argument on almost all real life processes.

In case of your broken rubber band, it won't be attached again to become as before even if you try to undo all energy changes you did at molecular level (holding pieces together is also such try).

The key to all is entropy change. So, the answer to your question: The rubber band won't be attached again automatically because entropy of system would be decreased by that.

And, don't underestimate entropy thing. It is discussed in high-level theories like string theory, QFT. Entropy change is sometimes called "arrow of time".

Answer 4

Many of the proposed answers focus on entropy and the low probability of all the microscopic components of the process coming together to result in a reformed band. I'm not convinced these answers get to the second part of your question: given infinite time will the band be reformed? Before coming to my approach to answering your question, a brief look at rubber.

Some chemistry

Let's assume that the rubber band is made out of natural rubber, which is a polymer of isoprene with some impurities in it. We'll ignore the impurities. The isoprene polymer, or polyisoprene, looks like this:

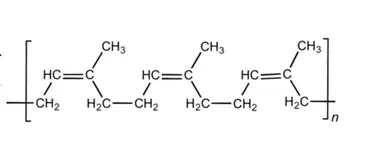
These long chains (n is easily > 10^4) can slip and slide across one another, and without any stability make for a really crappy material for holding things together (a chewed piece of gum molded into the shape of a band would have better elastic and stability properties). To add stability and elasticity to natural rubber, the polymers are crosslinked through vulcanization. Sulfur is added and makes bridges between neighboring polymers, allowing them to move but not get too far away. The crosslinked polymers look something like this, although note that the actual material wouldn't have as high of a sulfur density as depicted in this figure

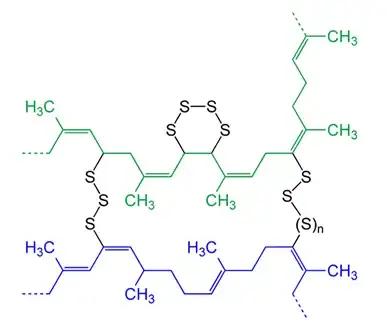
Some reactions

Let's walk through your thought experiment. When the rubber band is stretched to the point of breaking, chemical bonds are broken. Looking at the cross-linked image above, the options are S-S bonds, S-C bonds and C-C or C=C bonds. Looking at the bond dissociation enthalpies we see that the S-S and S-C bonds are the weakest of the set; so in all likely hood, the bonds that are being broken are the bonds added through the vulcanization/cross-linking process.

In an oversimplified picture, we can express rubber band breaking like this:

$$formed\ band \rightleftharpoons broken\ band \\ S-C \rightleftharpoons S\cdot +\ C\cdot$$

I use double arrows here because in your thought experiment, we are assuming that the band breaking is a reversible processes. Given that bond breaking requires energy, it stands to reason that your conjecture has some merit; namely, bond formation is energetically feasible and given enough time should occur, resulting in a reformed band.

Some thermodynamics

Chemical reactions can occur under thermodynamic or kinetic control. I interpret your statement "...given infinite time..." as what is the product of this reaction under thermodynamic control?. We therefore need to look at the Gibbs free energy of the bond dissociation reaction to determine the thermodynamically favored products ($S\cdot + C\cdot$ vs. $S-C$, or broken band vs. whole band). For a thermodynamically favorable process, $\Delta G = \Delta H - T\Delta S$, $\Delta G$ must be negative. For bond breaking, $\Delta H$ is positive and $\Delta S$ is positive, meaning that $\Delta G$ is negative when $T \Delta S$ is greater than $\Delta H$. We can therefore claim that there is a temperature at which breaking of the rubber band is thermodynamically favorable. Intuitively this makes sense: heat up the rubber band, eventually it will no longer be a rubber band. Since we are interested in the reverse reaction, we change the signs of the thermodynamic properties and bond formation (band repairing) would be thermodynamically favorable at low temperatures (although that low temp may have to be very close to absolute zero at which point chemistry starts getting weird).

Conclusion

So I think the key to this question is your use of the term infinite, which moves us from a kinetic regime to a thermodynamic regime. I'm also making some pretty hefty assumptions (e.g. approximating band breaking/forming with a single type of bond breaking/forming) which may be too broad. Under these constraints, the thermodynamics suggest that a formed band is more favorable than a broken band. If my model is overly simplified, you can use the same process with more conservative assumptions.

In reality, these type of thermodynamic thought experiments aren't terribly helpful. Diamond, for example, is more thermodynamically stable than graphite. I'm not going to win over the girl-next door by giving her pencil and saying, "my love for you is as eternal as this diamond will be". As soon as you move back into the realm of finite time, kinetic control is going to take over, and the energy barriers to rubber-band formation are going to be too high for the repair to happen.

Answer 5

You have broken the chemical bonds between the molecules by inserting energy which is then dissipated. You also distorted the molecule structure. To repair this you should again insert energy. Holding the pieces together does not provide the energy, nor reorders the molecule structure. The answer to your second question is this no.

Answer 6

Exact mechanism varies with material. Simple materials (non-organic) are easier to analyze. Simplest answer is if you bring them together they will join, provided size is small. For example in Cold Welding less than 10 nm wire is rejoined just by contact. The exact mechanics depends on what kind of Intermolecular force is in play.

According to Grove Karl Gilbert

To my mind it appears that the difference is only imaginary and not real. Rigidity and plasticity are not absolute terms but relative, and all solids are in fact both rigid and plastic. The apparent contrast between the two properties belongs to the laboratory and to those phenomena of nature involving small masses and small forces. When great masses and great forces are involved, as for example in the making of continents and mountain chains, the distinction loses value. The phenomena of mountain structure demonstrate that under sufficient strains great bodies of rock both bend and flow.

Its some what explained in this video