As we know, The double pendulum has a chaotic motion. But, why is this? I mean, the mass of the two pendulums are the same and they have the same length. But, what makes its motion random?
I'm just a high school kid. So, try to make answers understandable.
Chaotic is not the same as random. A chaotic system is entirely deterministic, while a random system is entirely non-deterministic. Chaotic means that infinitesimally close initial conditions lead to arbitrarily large divergences as the system evolves. But it's impossible, practically speaking, to reproduce the same initial conditions twice. Given enough time, two identical setups, set to initial conditions that are as identical as possible, will look entirely different.
Perhaps a better question to ask is: why is a single pendulum non-chaotic? Almost all real systems are chaotic at least to some extent; the fact that we can write out the solution for a single pendulum for all points in time is really quite peculiar, and only true because it is a highly simplified system. The reason these non-chaotic systems are so prevalent in textbooks is because historically, us humans with our peculiar mathematical toolset and limited abilities to calculate, have been aggressively looking for such idealized systems.
The cheap and easy answer to this is that the double pendulum is considered chaotic because it is very sensitive to small perturbations in initial conditions (amongst other things). Showing this mathematically may be difficult (see the Lagrangian formulation for the dynamics), but if one looks at the animations on the Wikipedia page showing the trajectory of the double pendulum, the intuitive reason for this sensitivity should become obvious. There are many points in the trajectory where the acceleration rate of the outer pendulum is very dependent on the exact angle of the upper pendulum as it is whipped around. If the inner pendulum is in a sightly different place, the outer pendulum is whipped around at a very different rate, changing how "coupled" the two pendulums are. Sometimes the effect is to tie them together like they were a string on a grandfather clock. Sometimes it causes them to be almost perfectly opposed in position, doing their own thing.
Every time it reaches one of these states, it becomes very sensitive to the initial conditions that lead it to that state. A sight perturbation along the way could have arbitrarily magnified effects later.
From a mathematical standpoint, deterministic chaos or sensitive dependence on initial conditions, is created when there are more than 2 dimensions or variables along with a sufficiently complex relationship between those variables, such as non-linearity and/or coupling.
There are 4 variables in a double pendulum, two angles and two angular velocities. The mathematical relationship between these variables involves squares (non-linearity) as well as sines and cosines (more non-linearity) of both angles in the same equation (coupling).
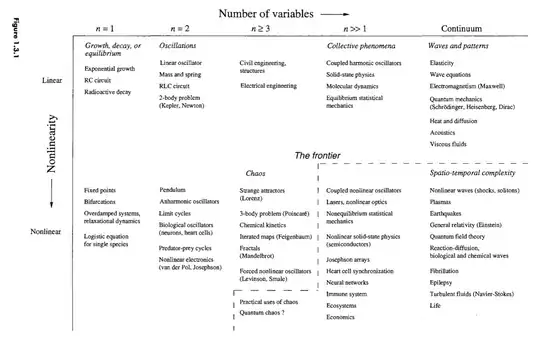
Image source: Strogatz, Nonlinear Dynamics and Chaos
