As far as I'm aware, there is no limit to the acceleration a particle (or anything else) can experience.
Why? Well, one may start looking at Newton's second law $F = ma$ and say, well, $a$ can be just as unbounded as $F$, right? Like Julian has said, tidal forces near black holes can become unbounded as you approach the singularity. Black holes are a general relativistic phenomenon though, so this equation is inadequate. Now when you enforce the postulates of relativity and assume $c < \infty$, relative acceleration is governed by the geodesic deviation equation:
$\frac {D^2 X^{\mu}} {dt^2} = R^{\mu}_{\nu \rho \sigma} T^{\nu} T^{\rho} X^{\sigma}$
where $T^{\mu} = \frac {\partial x^{\mu}} {\partial t}$. There is no apriori bound placed on how 'negative' the Riemann tensor is allowed to be; that is to say there are no mathematical results (assuming a $\it{really}$ generic space-time) that limit the behaviour of $R^{\mu}_{\alpha \beta \gamma}$, and hence the term on the LHS relating to acceleration.
However, with regards to the Heisenberg uncertainty principle, we must consider space-time to essentially be a discrete object, meaning we cannot infinitely divide up time and obtain a continuous limit (otherwise observations don't make sense). This in mind, no matter how small you make the time steps, we must limit the overall 4-velocity $v^{\mu}$ of the object to be bounded by $c$. So, acceleration must always be finite but can grow arbitrarily large, since we approximately have in a time-step $\delta t$: $v \approx a \delta t$.
Edit: What I really mean in this last paragraph is that it does not make sense to talk about motion in zero time. So, since $v < \infty$, and $\delta t >0$, we must also have that $a < \infty$ regardless of the theory of motion we are dealing with.
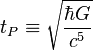 ~5.39106(32) × 10−44 s
~5.39106(32) × 10−44 s