Experimental Evidence of Random Tiling Limit Shapes

Question

In the area of random tilings, there are many results that fall under the term "Arctic Circle Theorems." This roughly means that if one chooses a tiling of a specific region uniformly at random, then there will generally be a boundary region outside which the tiles are "frozen" in a fixed configuration. Here are some computer generated examples:

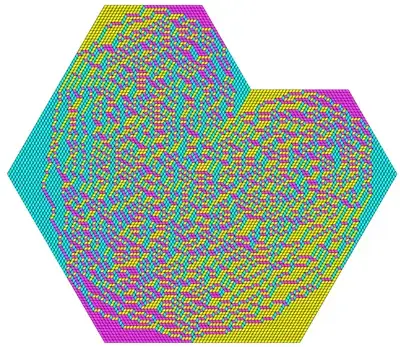
I keep seeing references in the random tiling literature to models in statistical physics but I've never actually seen a picture from an experiment. I've heard for example that random dimer models correspond to adsorption of a gas onto a thin film. I'd be thrilled to see some pictures of these limit shapes, from say a scanning electron microscope (obviously the tiles involved should be large enough to discern, so perhaps a gas is a bad example). I'm not asking for a bunch of examples, just one or two is more than enough. An example that would fit my criteria is one where the partition function is close to one of a random tiling model, such as dimers or rhombii.

Answer 1

I don't know if this answers your question.

Have you seen how a cube of ice melts? Focus on one corner and you will see the melting happening on the edges. This is precisely the limit shape that you get from the domino tiling of a hexagon (which can be mapped to the dimer problem). This is called the Wulff shape of a crystal. See also the (theoretical) article by Okounkov. The Arctic circle observed by Cohn, Kenyon and Propp is similar.