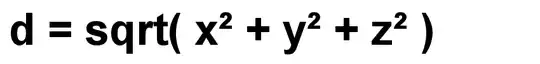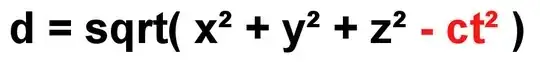How to determine "timelike"-ness without using a coordinate system?

Question

It has been stated here that:

we can say, without introducing a coordinate system, that the interval associated with two events is timelike, lightlike, or spacelike

.

This assertion appears at variance with

• the definition of "time-like (or light-like, or space-like) intervals" as defined here: http://en.wikipedia.org/wiki/Spacetime#Spacetime_intervals explicitly in terms of "differences of the space and time coordinates", and

• the definition of "curves" as "chronological (or timelike)", "null" (or "lightlike"), or "spacelike", and thus correspondingly of pairs of "points" of any such "curve" as "timelike (or lightlike, or spacelike) related to each other" of http://en.wikipedia.org/wiki/Causal_structure#Curves which explicitly requires the notion of Lorentzian manifold and thus according to http://en.wikipedia.org/wiki/Manifold#Mathematical_definition uses coordinates as subsets of $\mathbb R^n$ and their topological relations (as "coordinate system").

Therefore I'd like to know:
How can be determined whether the interval associated with two events (which are given or characterized and distinguished by naming, for either event, the distinct individual participants which had been coincident at that event) is for instance "timelike", without using any coordinates and coordinate system?

Is it correct that the interval associated with two events (given as described above) is "timelike" if and only if there exists at least one participant who took part in both of these events?

Answer 1

How about this for a more "physical" definition: two points in space-time are time-like separated if and only if a massive particle starting at one could, if subjected to appropriate finite forces, reach the other.

Replace "massive" with "massless" to get the definition of light-like separation. If neither is possible the the points are space-like separated.

Answer 2

A timelike interval between two events means that they can be causally connected, by influences that travel at less than the speed of light. In principle a physical clock could be transported at less than the speed of light from one of the events to the other and all observers would agree on the proper time that elapses on the transported clock. For this reason the interval is considered invariant.

A spacelike interval between two events means the events cannot be causally connected and they are outside each others light cones.

A lightlike interval between two events means that any causal influence between the two events must have propagated at the speed of light.

Answer 3

Let $\lambda, \mu, \nu$ be functions on the reals to points (events) in spacetime. Let these be "straight" curves, in the sense that $\lambda', \mu', \nu'$ each all have the same direction for all values of their parameters. For example, $\lambda(u) = \lambda_0 + lu$ is a simple case, as $\lambda'(u) = l$. The vector $l$ is the vector along the direction of the straight curve.

Given these three straight curves, we can define events $A$, $B$, $C$ that are the intersections of $\lambda, \mu$; $\lambda, \nu$; and $\mu, \nu$. $A$ is point defined by the parameters $u, v$ such that $\lambda(u) = \mu(v)$. If some material objects are following these worldlines, then the objects meet at these intersections, at these events.

The rest of the process of determining whether the interval between, for example, $A$ and $B$ is timelike, spacelike, or lightlike is then similar to Julio Parra's answer: say we want to determine whether the interval between $A$ and $B$ is spacelike, timelike, or lightlike. The common worldline between these two events is $\mu$. We would then integrate the derivative to find the length of the spacetime interval between these two events along the worldline $\mu$:

$$s^2 = \int_{v_A}^{v_B} \eta[\mu'(v), \mu'(v)] \, dv$$

And the sign of $s^2$ then determines whether the interval is spacelike, timelike, or null (it depends on the metric).

I think the key point is the identification of some connecting straight worldline between two events--some "observer" or "participant" who takes part in both events of interest. EDIT: no other connecting worldline will give the same answer, but the worldline that extremizes the answer is considered canonical for defining this quantity. In the flat spacetime case, that's the straight path.

In general, we can talk about whether vectors are spacelike, timelike, or lightlike without considering two particular events. These are properties of directions in spacetime, not necessarily pairs of events.

Answer 4

For example:

From "Gravitation and Spacetime" via Google Books

---

Added to address a comment below:

My question was intended to be addressed without referring to any coordinates; including no coordinates (!) such as "clock times T, T1, T2" or somesuch.

But these clock times aren't coordinates. The reading of a single clock is the proper time along the worldine of the clock, i.e., it is an invariant and coordinate independent measure of time. From the Wikipedia article "Proper Time":

In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events.

Moreover, in the 2nd paragraph of the text above we have:

The radar-ranging procedure permits us to bypass the coordinate system, so we can measure the spacetime interval without the use of coordinates.

Consider a clock at rest with respect to you. The 3 orthogonal spacelike directions are evident as is the (Lorentzian) orthogonal timelike direction. The ticks of the clock gives a proper time parameter along the timelike worldline of the clock.

We can define the coordinate time, in the frame in which the clock is at rest, as the proper time given by the clock. And, we can define space coordinates as described above.

In your comment, you put the cart before the horse. The coordinates were defined by the direct measurement of the interval, not the other way around.

Answer 5

One has not necessarily to know all this quantitative interval stuff to distinguish time-likeness. Suppose an observer lives on a body without (significant) atmosphere, such as our Moon. All events observed by means of light (EM radiation) belong to observer’s light cone and hence are separated by a null interval from the observer. All events observed indirectly (either by reflected or scattered light, or by their material traces) belong to observer’s past cone and hence are separated by a time-like interval from the observer. Events separated by a space-like will not be seen in any way, as well as the entire future cone (with both null and time-like intervals). But the observer can influence events of the future cone, whereas events with space-like intervals are inaccessible in any direction, from observer’s present moment.

Suppose, we pinged our lunar resident-observer (event P), he replied (event Q), and we received the reply (event R). Intervals P–Q and Q–R are null. Interval from anything on Earth before P and Q is time-like, with Q at the future end. Interval from Q and anything on Earth after R will also be time-like, with Q at the past end. Intervals from Q and our history between P and R are space-like: neither can our resident-observer at Q know anything about P⋯R (P excluded), nor can it influence anything in P⋯R (R excluded).

Ī answered the question with respect to the physical spacetime. If the question is about mathematical formalism to deal with spacetime without coordinates, then examples from the previous paragraph can be interpreted as a partial order relation.

Answer 6

Jee-ziss, the answer is simple.

The interval metric is a pseudometric. That means it has two components, the space component and the elapsed time component. If the time component is larger, the interval is timelike.

That's it.

Why this is true:

Normal Euclidian space has three dimensions, all of which add distance to the total distance if a vector has a component that extends into that direction.

We say that Euclidean space has a "metric signature" of (3).

But not all spaces are Euclidean. In particular, our spacetime is not euclidian; it's Lorenzian.

To describe its number of dimensions, you have to use an expanded version of the metric signature: (3,1). This means spacetime has three positive dimensions, and one dimension that's negative.

In this kind of space time, the elapsed-time component is subtracted from the space component:

Mathematically, elapsed time acts like negative distance.