How to read WSJ US Treasury quotes

Question

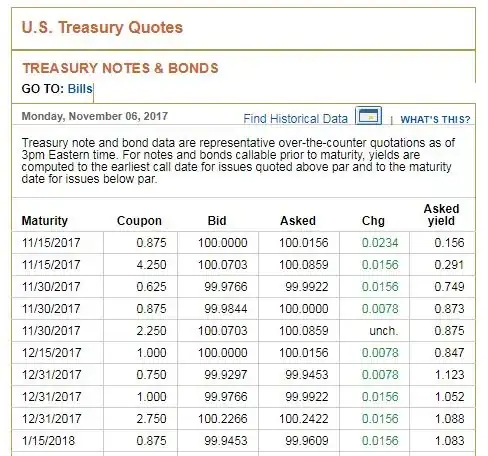
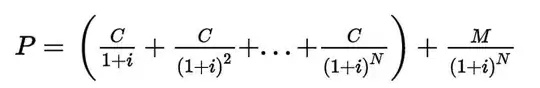I am trying to understand how they calculated "asked yield". If anyone can explain it, I really appreciate it. I would like to see the mathematical formula and the calculation.

Answer 1

0 The ask yield is

annualized percentage return that the purchaser will receive if the note is purchased on the day of the quotation at the ask price and held until maturity.

This is called the (annualized) yield-to-maturity, which is just the effective interest rate (i) that you get if you bought the bond today and took all the coupons never selling it. There is formula for the price of bond where C is the coupon, M is the payment at maturity and P is the present value...

This appears a little complicated but it looks like you just have to solve for i in this equation (annualize it) and you would be done. The problem is this equation has no simple solution. You have to use a specialized financial calculator to solve it, but your problem is actually even harder than that. Let's see why...

Let's take your first line, C would equal C=0.875/2 (half the coupon because it is paid twice a year) P=100.0156 (ask price), M=100 (value of a treasury at maturity) and the number of periods N is... crap this is more complicated.

We have a bond that matures in 9 days so we have a partial period and calculate the accrued interest so C is really C=0.875*(9 days/365 days) and now N=0 since we have no full coupons left. Now, you can solve for i is you are mathematically inclined, but for bonds with longer time left N>0 and we need that financial calculator again.

After all this you still have to annualize i on a 365 day basis, not hard compared to the above, but still a lot for a stack exchange answer.

You can see why professionals use specialized software or just rely on Bloomberg or the WSJ. But while this is all a complicated calculation the idea is simple. The ask yield is just the yield you get buying the treasury now and holding and we annualize this yield so investors can easily compare one treasury to another.