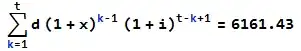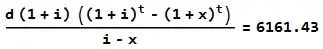4

I'm looking to solve this problem:

If I were to start investing now, With a 4% annual return compounded monthly what is the function for my return if my monthly input is initially $2000 then for every month here after 2% is added. For example:

month 1 deposit = 2000

month 2 deposit = 2040

month 3 deposit = 2080.80 etc.

I understand the compound interest formula with a uniform monthly deposit to be:

p*(i+1)^t + d * ((1+i)^t - 1)/(i) * (1+i)

where p is our initial value, t is the number of compounding periods and d to be the periodic deposit. But I'm struggling to find the formula with the increase in the monthly deposit.

I have a feeling that there isn't a straight forward formula (I hope to be shown wrong!) but maybe it is possible to write a python script with a loop or a rrnewing d variable?

Brythan
  • 20,986
  • 6
  • 54
  • 67
Griffin Kennedy
  • 41
  • 2

1 Answers1

2

Disregarding the initial value p for the moment

the monthly interest rate i = 0.04/12

so with initial deposit d = 2000 the value after three months is

d (1 + 0.02)^0 (1 + i)^3 +
d (1 + 0.02)^1 (1 + i)^2 +
d (1 + 0.02)^2 (1 + i)^1 = 6161.43

This can be expressed as a summation with

t = 3
x = 0.02

enter image description here

and the summation can be converted to a formula by induction

enter image description here

Adding the initial value compounded over three months p (1 + i)^t

future value = p (1 + i)^t + (d (1 + i) ((1 + i)^t - (1 + x)^t))/(i - x)
Chris Degnen
  • 10,107
  • 1
  • 21
  • 36