Balances above $5,000 earn a simple interest rate of 0.10%, with a corresponding APY of 2.54%-5.00% APY.
I don't understand how a simple interest rate that is a fixed number can result in a range of APYs, especially one that varies over the range by almost a factor of 2.
What is the meaning of this statement, and how does the math work out?
It appears that qualifying accounts up to $5,000 earn 5% APY. Anything above $5,000 earns 0.1% (apparently per annum), so a total balance of $10,000 earns 5% APY on one half and 0.1% on the other half. After one year that is
(5000 * 0.05) + (5000 * 0.001) = 255
so 2.55% APY on $10,000.
However, with higher balances the APY goes below 2.54%. In order to achieve a minimum APY of 2.54% the balance above $5,000 needs to yield 2.5397% APY. It's not clear how that can relate to "simple interest" at 0.1%.
x = Balance
APY = 100 (Min[5000, x] * 0.05 + Max[0, (x - 5000)] * 0.025397) / x
Perhaps there is a maximum balance allowed which limits the APY.
If you would've copied to sentence before this sentence, it would be quite obvious:
UltimateAccount annual percentage yield (APY) is 5.00% on balances up to $5,000. Balances above $5,000 earn a simple interest rate of 0.1 %.
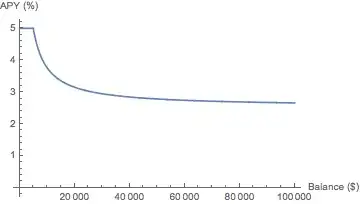
So if your total is below 5000, you get 5%. Above 5000 you get 0.1%. Depending on your total, the average is between 5% and 0.1%; the more you have, the lower.
If you put 10000 in the account, the first 5000 give 5%, and the remaining 5000 give 0.1%, which adds to 5000*5%+5000*.1% = 250+5 = 255 = 2.55% of 10000 (The small difference to 2.54 is either rounding error, or comes from them only giving interest for 360 days instead of 365 per year (which is usual), and the APR is defined by law to reflect the annual effective rate.
If you put any number between 5000 and 10000 in the account, the summary APR lies between 5% and 2.55%. For example 6000 gives: 5000*5%+1000*.1% = 250 + 1 = 251; 251 of 6000 is 4.183%. If you use 7000, you get 5000*5%+2000*.1% = 250 + 2 = 252; 252 of 7000 is 3.6%. You should be able to repeat this math for any other number.
Each number between 5000 and 10000 gives an overall APR between 5% and 2.55%; the larger the input, the lower the average APR.
Note that that implies that either they assume nobody would put more than 10000 in such an account; or they assume this limit for cosmetic reasons (otherwise it would read '0.1 - 5%' APR, much uglier...); or the fine print states that there is no interest after 10000 at all.
Aganju's response above is spot-on. The rationale for the range of APY is 'banking compliance regulations.' Our regulators require for the disclosure of what APY you could earn. Our Ultimate Account has tiered interest rates so if your balance was $5,000 all month, you could earn 5.00%. But if your balance was $10,000 then the corresponding APY would be 2.54%. Obviously there are countless iterations you could insert here for every balance possibility but the disclosure copy you see on our website is what our compliance folks felt best addressed the required deposit product advertising regulations.
I realize the explanation above may not have cleared up how the numbers are what they are but it should explain why you see a range of APY figures quoted.
Sincerely,
Bill Clancy, Northpointe Bank
