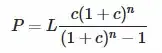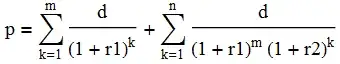8

Can people tell me how monthly payments are calculated when a mortgage has an initial rate?

What is the formula?

I have seen online calculators but not formulae.

My guess is:

We assume that the principal amount paid off each month in the inital period is as if the mortgage has no initial rate, then the payment in the initial period is adjusted for the (often lower) initial rate interest. Is this correct?

For example, let's assume I have a 25 years mortgage, which is on 3% for first 5 years, then 4% on the remaining term. How do we calculate the payment?

Ben Miller
  • 116,785
  • 31
  • 330
  • 429
Lost1
  • 193
  • 1
  • 1
  • 6

2 Answers2

13

In an adjustable rate mortgage (ARM), the starting interest rate is guaranteed for a certain period. After this period, the rate can go up or down.

The monthly payment on these loans is calculated as if the rate never changed over the life of the loan. However, if the rate does change, the monthly payment also changes to cover the change in interest so that the mortgage is still paid off in the same amount of time.

Using your example, let's say that you have a 25-year mortgage that is a 5-year ARM. The initial interest rate is 3%, which means that for the first 5 years, your rate is fixed at 3%. The monthly payment for those first 5 years is the same as it would be if you had a 25-year fixed rate mortgage at 3%. Here is the formula:

MathJax formula: $$P=L\frac{c(1+c)^n}{(1+c)^n-1}$$

where:

  • P = monthly payment
  • L = Loan amount
  • c = monthly interest rate. This is the annual interest rate divided by 12.
  • n = number of months in the loan (years * 12)

In our example, if the loan is $100,000, the interest rate is 3% (monthly interest rate is 0.25%, or 0.0025), and the number of months is 300 (25 years), the monthly payment will be $474.21.

Now, 5 years into a 25 year mortgage, the amortization schedule tells us that the remaining principal will be $85,505.48.

So if the rate jumps to 4% at that point in time, the monthly payment will be recalculated so that the loan is still paid off in the original 25-year time. To find the new payment, use the above formula again, but this time L=$85,505.48, c=0.04/12=0.0033333, and n=20*12=240. The new monthly payment is $518.15.

If, instead, you had a loan where the payment will be constant over the entire loan period, but the interest rate changes during the period (this is not common), there is a formula for that as well. See this StackOverflow question for the details.

Community
  • 1
Ben Miller
  • 116,785
  • 31
  • 330
  • 429
5

Normally in a variable rate mortgage the payment would vary with the rate. However here is a formula for a fixed payment, (where, as the OP says, the rate adjustment is known in advance):

d = (p r1 (1 + r1)^m r2 (1 + r2)^n)/
 (-r1 + (1 + r2)^n (r1 + (-1 + (1 + r1)^m) r2))

where

d is the periodic payment
p is the loan amount
r1 is the periodic rate for the first m periods
r2 is the periodic rate for the next n periods

Here is how the formula is derived.

First, taking a simplified problem to show the workings more clearly.

Let's say a £100,000 loan repaid by 5 annual payments. The first 2 years at 3% and the following 3 years at 4%.

p  = 100,000
r1 = 0.03
m  = 2
r2 = 0.04
n  = 3

The loan amount is equal to the sum of the present value of the payments. These are the present values of the payments for each period, discounted by the interest rate(s):-

pv1 = d/(1 + r1)
pv2 = d/((1 + r1) (1 + r1))
pv3 = d/((1 + r1) (1 + r1) (1 + r2))
pv4 = d/((1 + r1) (1 + r1) (1 + r2) (1 + r2))
pv5 = d/((1 + r1) (1 + r1) (1 + r2) (1 + r2) (1 + r2))

And p = pv1 + pv2 + pv3 + pv4 + pv5

This can be expressed as a summation

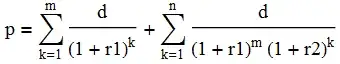
enter image description here

and converted to a formula by induction:

p = ((1 + r1)^-m (1 + r2)^-n (-d r1 + 
      d (1 + r2)^n (r1 + (-1 + (1 + r1)^m) r2)))/(r1 r2)

Rearranging to give a formula for the payment:

d = (p r1 (1 + r1)^m r2 (1 + r2)^n)/
 (-r1 + (1 + r2)^n (r1 + (-1 + (1 + r1)^m) r2))

∴ d = 22078.67

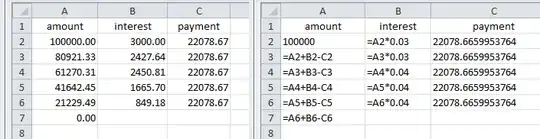
Amortization table for the above result showing figures and formulas

enter image description here

Returning to the OP's example for, say, a loan of one million, with the effective rate of interest at 3% for the first 5 years and 4% for the following 20 years.

p  = 1,000,000
r1 = (1 + 0.03)^(1/12) - 1 = 0.00246627
m  = 5*12 = 60
r2 = (1 + 0.04)^(1/12) - 1 = 0.00327374
n  = (25 - 5)*12 = 240

The payment d = 5026.48

Note for the use of nominal rates

For nominal interest rates of 3% and 4% compounded monthly:

p  = 1,000,000
r1 = 0.03/12 = 0.0025
m  = 5*12 = 60
r2 = 0.04/12 = 0.00333333
n  = (25 - 5)*12 = 240

The payment d = 5057.80

Community
  • 1
Chris Degnen
  • 10,107
  • 1
  • 21
  • 36