How are stock options priced?

Question

I was reading the Wikipedia article about the Black-Scholes model, and it says this:

The key financial insight behind the equation is that one can perfectly hedge the option by buying and selling the underlying asset in just the right way and consequently "eliminate risk".[citation needed] This hedge, in turn, implies that there is only one right price for the option, as returned by the Black–Scholes formula (see the next section).

Does this mean that an option is priced in such a way that the buyer and seller of the option should not turn a profit or a loss?

Also how would one hedge the option through buying and selling the underlying asset in order to eliminate risk?

Answer 1

Options pricing is related to game theory.

In sports, you like the Reds, I like the Greens. We wish to bet on a game. We can choose points to give the lower team's final score in order to make such a bet 50/50. Or knowing my Greens are far superior, I offer you odds. "If your Reds win, I will pay you 10 times your bet."

The B-S model does a good mathematical job of looking at historic volatility, and determining the odds of a price being exceeded in a given timeframe.

In October 2009 I wrote an article Will Gold Break $1250 by 2011? in which I described a strategy offering a 4 to 1 return if gold would increase 25% just over a year out. The options market literally said "give us $2400, and if gold closes over $1250 next January, we will give you $10,000." Similar betting was available on the downside. The market thought such a move over the 15 months was not likely.

My friend Nassim Taleb will tell you that the market, any market, does not follow the bell curve the math produces. That six-sigma event should occur every million years, but in fact, occurs far more often. I have nothing against the model, so long as you understand what it is and what it isn't.

Answer 2

Profit or loss from the option is a different subject and depends on where the underlying is relative to the strike price at expiration.

What the Wikipedia section discusses is that one can (dynamically) replicate the payoff of the option, thereby obtaining a (fair) cost for the option. As a result, one can hedge out all of the price movements related to the drift of the stock and the price of the option only depends on the risk free rate only (and the other parameters entering into the Black Scholes equation).

Black Scholes computes the cost of implementing this strategy (the price of the option and the cost of the strategy must be identical, otherwise there would be arbitrage).

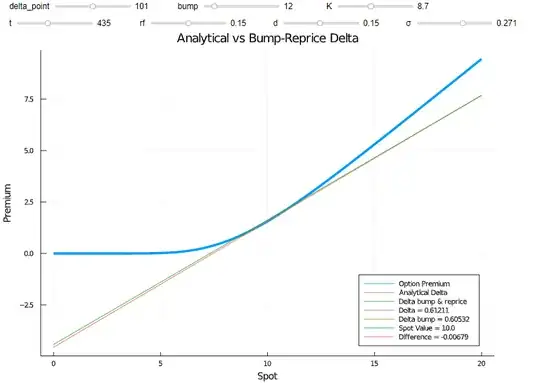
Hedging the option by buying / selling the underlying is called delta hedging. If you own a call option, you sell an amount of the underlying equal to delta. That way, if the price of the underlying increases, you gain with the option, but lose money in your underlying position. The total effect is roughly zero (for small changes in the underlying). The screenshot below shows delta, which is a linear approximation to the option price. As you can see, the difference between the actual change in the option value and the change according to delta is small as long as the change in the underlying is small (you can igore the bump & reprice part, this screenshot was just taking from another answer).

In the continuous time, dynamic hedging world of Black Scholes, this will work perfectly. It is not possible to do this in a real world setting and an interesting thought is the so called the Hakansson's paradox.

Either way, if you use Black Scholes, you can either plug in option prices and solve for (IV) implied vol (the standard way for price quoted exchange traded options) or plug in implied vol quotes to get the price (most OTC options are IV quoted or rely on computed vol surfaces). What you should not do is to use historical vol in the Black Scholes equation because this will typically misprice options and be of little use.