What's the formula to calculate the monthly or lump-sum investment amount for a desired future value?

Question

Give the following values:

• Inflation Rate 2%
• Expected Return Rate 5%
• Future Value 1,000,000 monetary units
• Years to Target - 10

What is the formula to calculate the amount of?

• Lumpsum investment
• Monthly investment

Answer 1

It's not entirely clear what you're asking... If you're talking about an Excel Formula for getting both of those, then:

=PV( Rate, NPER, PMT, Future Value)

=PMT( Rate, NPER, Present Value, Future Value)

For the lump sum investment, you would put the final value you need in as "present value", and the Payment would = 0.

For the Monthly Investment (with no up-front lump sum), you would put the monthly investment as the payment, and 0 for the Present Value. The Future Value is still the same.

---

If you're interested in doing the math, the formula for a Future Value of a Lump Sum is:

FV = (Present Value) * (1 + r)^n 

The formula to calculate the monthly payments to achieve a Future Value is commonly called a "Sinking Fund Payment":

PMT = ( FV * r) / [(1+r)^n] - 1]

r = interest rate for the period, n = the number of periods. Make sure that the interest rate matches the investment's compounding frequency.

If you are calculating the value of an upfront investment and additional monthly investments, you have to do the calculations as two separate problems.

You can do the algebra to reverse the lump sum formula around for Present Value fairly easily, or you can find the answer on Wikipedia.

Present Value & Future Value

Answer 2

This is the 2nd edit to the Original post, as I write without thinking the formula for annuity payments had the wrong interest factor and growth factor as I divided the rate by 12 for monthly compounded rate (this is a common error in logic) the actual factors use annualized rates for interest and growth. This has now been fixed in the two different formulas I have in this post

This is an edit of the Original post that includes indepth explanation and accompanies code for two user defined Excel PV and PMT function that permit gradient in calculating annuity payment and the lump sum

Lump Sum

PV = FV (1+g)^9 (1+i)^-10

g = 2% per annum i = 5% per annum

The formula listed above is correct but since your future value of 1,000,000 includes the growth thus we would use the following form of the formula to find the initial investment

PV = FV (1+g)^-9 (1+i)^-10

Here we are discounting 1,000,000 at an interest rate for 10 periods then a further discount at growth rate of 9 periods

Monthly payment The formulas PV, FV, and PMT earlier had it wrong, it has been corrected now

PV = PMT [ 1 - (1+aey(r, c))^-(n) (1+aey(g, c))^(n) ] / (aey(r, c)-aey(g, c))

PMT = PV (aey(r, c)-aey(g, c)) / [ 1 - (1+aey(r, c))^-(n) (1+aey(g, c))^(n) ] 

g = 2%/12 per month i = 5%/12 per month

The above formula helps find the payment that grows by a rate and earns interest when initial investment is known. When you have only final or maturity value of the investment then the following formula is used.

The formulas posted earlier had errors that have now been fixed

FV = PMT [ (1+aey(r, c))^(n) -  (1+aey(g, c))^(n) ] / (aey(r, c)-aey(g, c))

PMT = FV (aey(r, c)-aey(g, c)) / [ (1+aey(r, c))^(n) -  (1+aey(g, c))^(n) ]

The annual effective yield for interest and growth is calculated as follows

aey(r,c) = [(1+r/c)^c] - 1
aey(g,c) = [(1+g/c)^c] - 1

The formulas for PV, FV and PMT that are listed above will only find the correct results when period is in units of 1 and compounding is in units of 1. or if these units are the same

But when period gets defined as a fraction of a year such 1/12 for month and compounding frequency is selected such as 1/4 for quarterly then these formulas will not work

The VBA code uses a different formula which happens to be the sum of sequences of geometric series to find the correct answer. This is quite complex work as when you have periods with a fractional part such as 25.75 then to find the present value for 0.75 requires difficult calculations. It gets even more complex with arithmetic gradient whose closed form formula is listed below but its open form formula requires alot of work

PV = { PMT [ 1 - (1+aey(r,c))^(-n) ] / aey(r,c) } + Gradient/aey(r,c) { [ 1 - (1+aey(r,c))^(-n) ] / aey(r,c) - n (1+aey(r,c))^(-n)}

Excel does not offer options for inflation adjusted values, there are however 3rd party Excel add-in such as tadXL that permit Arithmetic and Geometric gradients in the time value of money calculations

But since Excel TVM functions have no way of adjusting for inflation, I will here offer you a slim down version of tadPV and tadPMT function that allow for a geometric gradient. The actual TVM functions in tadXL allow for not only a geometric gradient but also an arithmetic gradient (linear growth). And then those functions are much more complicated as they allow for growth period that does not co-incide with the payment period. And further they allow for a gradient thay may not begin immediately. Even without these options the following code offers much more as compared to Excel PV and PMT functions.

These functions allow you to define the period (length of the period) such as year=1, quarter=1/4, month=1/12, fortnight=1/26, week=1/52, day=1/365, binenial=2, triennial=3, and so on

These functions allow you to enter the compounding frequency of iterest such as yearly=1, quarterly=1/4, monthly=1/12, fortnightly=1/26, weekly=1/52, daily=1/365, infinite=0, biennial=2, triennial=3, and so on

You may also specify the discounting convention of your choice such as full-year=1, mid-year=1/2, 3rd Qtr=3/4, Biennial=2 and so on

Here are the results from your data

Lump Sum

=tadPV(5%, 2%, 10, 0, -1000000)
$513,695.15 

Monthly Payment

=tadPMT(5%, 2%, 10*12, 0, -1000000, 1, 1/12, 1/12)
$4,795.73 

Here is the code.

' Author: Abraham A.
' Publisher: http://thinkanddone.com

Public Function tadEFFECT(ByVal rate As Double, ByVal compounding As Double) As Double
If compounding = 0 Then
    tadEFFECT = Exp(rate) - 1
Else
    tadEFFECT = (1 + rate * compounding) ^ (1 / compounding) - 1
End If
End Function

Public Function tadFVIF(ByVal rate As Double, ByVal n As Double, ByVal compounding As Double) As Double
    tadFVIF = (1 + tadEFFECT(rate, compounding)) ^ (n)
End Function

Public Function tadPVIF(ByVal rate As Double, ByVal n As Double, ByVal compounding As Double) As Double
    tadPVIF = (1 + tadEFFECT(rate, compounding)) ^ (-n)
End Function

Public Function tadPVIF2(ByVal r As Double, ByVal n As Double, ByVal c As Double, ByVal p As Double, ByVal d As Double) As Double
Dim t As Double

t = 0#

t = (n - 1) * p + d * p
If (r = 0#) Then
    tadPVIF2 = 1#
Else
    tadPVIF2 = tadPVIF(r, t, c)
End If
End Function

Public Function pvifga(ByVal r As Double, ByVal g As Double, ByVal n As Double, ByVal type1 As Integer, ByVal c As Double, ByVal p As Double, ByVal d As Double) As Double

Dim pvifa, t, gt, remaining, aif, af1n, af1d, af2n, af2d, af1, af2, af, N0, N1 As Double
Dim i As Long

    pvifa = 0#
    t = 0#
    gt = 0#
    remaining = 0#
    aif = 0#
    af1n = 0#
    af1d = 0#
    af2n = 0#
    af2d = 0#
    af1 = 0#
    af2 = 0#
    af = 0#
    N0 = 0#
    N1 = 0#

remaining = n - Int(n)

For i = 0 To Int(n) - 1

    If (type1 = 0) Then
        t = i * p + d * p
    Else

        If (i = 0) Then
            t = 0
        Else
            t = (i - 1) * p + d * p
        End If
    End If

    If (i = 0) Then
        gt = 0
    Else
        gt = (i - 1) * p + d * p
    End If

    pvifa = pvifa + tadFVIF(g, gt, c) * tadPVIF(r, t, c)
Next i
N1 = (n - 1) * p + p * d
N0 = (Int(n) - 1) * p + p * d
If (remaining <> 0#) Then
    If (r = g) Then
        af1n = n * (1# + tadEFFECT(r, c) * type1) ^ (p * d)
        af1d = (1# + tadEFFECT(g, c)) ^ (p * d)
        af2n = Int(n) * (1# + tadEFFECT(r, c) * type1) ^ (p * d)
        af2d = (1# + tadEFFECT(g, c)) ^ (p * d)
        af1 = af1n / af1d
        af2 = af2n / af2d
        af = af1 - af2
    Else
        aif = (1# + tadEFFECT(r, c) * type1) ^ (p * d)
        af1n = tadFVIF(g, N0, c) * tadPVIF(r, N0, c)
        af1d = (tadEFFECT(r, c) - tadEFFECT(g, c))
        af2n = tadFVIF(g, N1, c) * tadPVIF(r, N1, c)
        af2d = (tadEFFECT(r, c) - tadEFFECT(g, c))
        af1 = (aif * af1n) / af1d
        af2 = (aif * af2n) / af2d
        af = af1 - af2
    End If
    pvifa = pvifa + af
End If
pvifga = pvifa

End Function

Public Function tadPV(ByVal rate As Double, ByVal gradient As Double, ByVal nper As Double, ByVal pmt As Double, ByVal fv As Double, Optional ByRef type1 As Integer = 0, Optional ByRef compounding As Double = 1, Optional ByRef period As Double = 1, Optional ByRef distribution As Double = 1) As Double
    tadPV = -fv * tadPVIF2(rate, nper, compounding, period, distribution) * tadPVIF2(gradient, nper-1, compounding, period, distribution) - pmt * pvifga(rate, gradient, nper, type1, compounding, period, distribution)
End Function

Public Function tadPMT(ByVal rate As Double, ByVal gradient As Double, ByVal nper As Double, ByVal pv As Double, ByVal fv As Double, Optional ByRef type1 As Integer = 0, Optional ByRef compounding As Double = 1, Optional ByRef period As Double = 1, Optional ByRef distribution As Double = 1) As Double
    tadPMT  = ( -pv - fv * tadPVIF2(rate, nper, compounding, period, distribution)  * tadPVIF2(gradient, nper-1, compounding, period, distribution) ) / pvifga(rate, gradient, nper, type1, compounding, period, distribution)
End Function

Answer 3

Using APR as defined here, and neglecting inflation for the demo calculations.

Note

To account for inflation inflate the target final value (f) accordingly. I.e. aim for final value

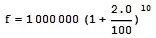
Periodic investments (m) would continue to be made at the face value, unaffected by inflation.

The demo calculations

The periodic investment case assumes periodic investments up to the time that the target final value is achieved.

Answer 4

And to figure out the Payment for a given FV, you cannot 'reverse' the formula given (FV for a stream of payments), but have to do some guessing and iterate to refine your guesses. Binary iteration is easiest (but takes more iterations than more sophisticated iteration methods). I seem to remember that Excel does offer a 'solve by iteration' tool.

Binary Iteration: If you know that Payment is between X and Y, then try with the midpoint of this range and see which half of this range the Payment value lies within. Then try again with the midpoint of your new range. And again, and again.

FV in your case would be adjusted for inflation as 1M*(1.05)^n.

Note that there is no 'indexing' of payments to inflation in this formula.

I assume you are not just interested in the answer for the case where Interest = Inflation? Because then it would just be Payment = FV/n.