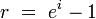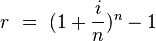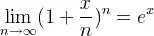10

A common explanation for the mathematical constant e (2.71828...) is that it is the factor by which an investment would grow at 100% interest rate over a period if it is continuously compounded.

In other words, if you were to invest 1 million dollars for one year at a rate of 100%, after one year, the balance would show about 2.71 M$ (or e M$)

However, it is not a case I have ever seen. We often see monthly compounding, sometimes daily, but I've never seen continuous compounding.

Does continuous compounding exist in practice? Is it ever part of a financial product offering? If so, in which cases might it be used?

Chris W. Rea
  • 31,999
  • 17
  • 103
  • 191
jonallard
  • 201
  • 2
  • 5

2 Answers2

9

Continuous compounding at an interest rate of 100% is unlikely to be used in practice. More generally, if the interest rate is x% per annum and interest is compounded n times during the year (so that at the end of each sub-interval, the amount increases by a factor of (1 + (x/100)/n) ), then the amount has increased over the year by a factor of

(1 + (x/100)/n)^n which is approximately e^(x/100) = 1 + (x/100) + (x/100)^2/2 + (x/100)^3/6 + .... when n is large.

Mathematically, e^(x/100) is the limiting value of (1+(x/100)/n)^n as n tends to infinity. Heuristically, (1 + (x/100)/n)^n gets closer and closer to e^(x/100) as n gets larger and larger (from quarterly to monthly to daily to hourly .... compounding).

So, let us turn the problem around. If the annual percentage yield (not the same as the APR) is specified as y% per annum, then let x be the solution to the equation

e^(x/100) - 1 = (y/100)

which gives x = 100 log_e (1 + y/100)% as the rate that would be quoted as the APR for continuous compounding while the APR for monthly compounding would be quoted as the solution to

(1 + (x/100)/12)^12 = 1 + y/100

which gives x = 12 times 100 times the 12th root of (1 + y/100) % as the APR.

As a comparison, an annual percentage yield of 5% per annum corresponds to a quoted rate (APR) of 4.88894...% per annum compounded monthly and 4.8790...% per annum compounded continuously. Weekly and daily compounding would result in quotes somewhere in between these two figures, but as you can see, for a given annual percentage yield, continuous compounding really does not make that the APR significantly smaller than the more common monthly compounding used for mortgages, auto loans, and the like.

Dilip Sarwate
  • 31,788
  • 4
  • 56
  • 124
0

Here are some calculations for an investment which yields a final value of $ e million ($2,718,282) from an initial value of $ 1 m.

The logarithmic or continuously compounded return is given as:-

enter image description here

Vf = 2,718,282
Vi = 1,000,000
rlog = ln(Vf/Vi) = 1.0 = 100 %

This is a logarithmic return, or nominal return (continuously compounded) of 100%.

The effective annual rate can be calculated by:-

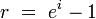
enter image description here

where i is the logarithmic or continuously compounded nominal rate.

i = rlog = 1.0 = 100%
r = e^i - 1 = 1.718282 = 171.8282 %

An effective annual return of 171.8282% produces the final value of $ e million.

Of course, the effective return can also be calculated as:

r = Vf/Vi - 1 = 1.718282 = 171.8282 %

Now considering monthly periodic returns

The effective annual rate calculated from a periodically compounded nominal return is:

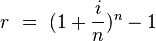
enter image description here

where n is the number of compounding periods.

Rearranging this formula, and using the previously calculated effective annual rate (which produced $ e million), the annual nominal rate compounded monthly is calculated:

r = 1.718282 = 171.8282 %
n = 12
i = n*((r + 1)^(1/n) - 1) = 1.0428486 = 104.28486 %

Note how this differs from the 100% calculated for the continuously compounded nominal rate. As n increases the periodic nominal rate approaches the continuously compounded nominal rate, as demonstrated by the limit formula:

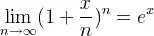
enter image description here

For example, the nominal rate compounded daily (with n = 365) is 100.137%, which is somewhat closer to 100% than the nominal rate compounded monthly.

From the annual nominal rate compounded monthly, the monthly compounding rate can be found:

m = i/n = 1.0428486/12 = 0.08690405 = 8.690405 %

Checking by compounding for 12 months: (m + 1)^n - 1 = 1.718282

The monthly compounding rate can also be calculated directly from the logarithmic rate, or annual continuously compounded nominal rate:

i = rlog = 1.0 = 100 %
n = 12
m = e^(i/n) - 1 = 8.690405 %
Chris Degnen
  • 10,107
  • 1
  • 21
  • 36