Suppose you’re day trading and the underlying is going up. You have a want a put though as you think it’s going down long term.
If you bought a 0DTE put, and the underlying moves in the opposite just a little, the premium drops through the floor on you. However if you bought a 10DTE, the premium drops less.
Is this because of Theta? Since the 0DTE is now less likely to be ITM as time is rapidly ticking away, and the 10DTE still has some time to be ITM?
You ask about how the price of the option changes with respect to the price of the underlying. This is Delta.
Intuitively, if an option is very close to or is At The Money (ATM = price of underlying is near-enough the same as the strike) and you're getting very close to expiry/expiration then there will be little chance that the price of the underlying will recover any move it might make.
In the case of your ATM Put, with zero days to expiry, pretty much any rise in the underlying price will make it much less likely the option will finish in the money, so its value will drop to zero very quickly. How sensitive the Delta is to moves in the underlying is Gamma. ATM options with little time remaining tend to have a very high Gamma. You can visualise this in a pay-off chart: the slope change from delta=0 (OTM) to delta=1 (ITM) gets much sharper as DTE gets less.
You're clearly aware of Theta, the time value of the option. Theta-decay gets more rapid as you get closer to expiry (1 day less from 2DTE is 50% less time, but 1 day from 10DTE is only 10% less). However for an ATM option close to expiry, the Gamma (and thus Delta) effect tends to dominate, and that's what you're describing with your ODTE Put.
With zero days to expiry, the value of the option with respect to the underlying is essentially a straight line kinked at the strike:
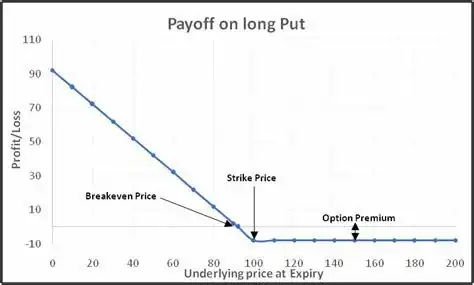
If the underlying price is below the strike (In-The-Money), the value of the option changes 1-1 with every change in the underlying, so the Delta is 1. If the underlying is above the strike (Out-of-The-Money), the option is worthless regardless of changes in the underlying, so the Delta is zero.
With 10 days to expiry, the value graph is no longer a straight line, but it now a smooth curve to account for the possibility of the underlying crossing the strike:
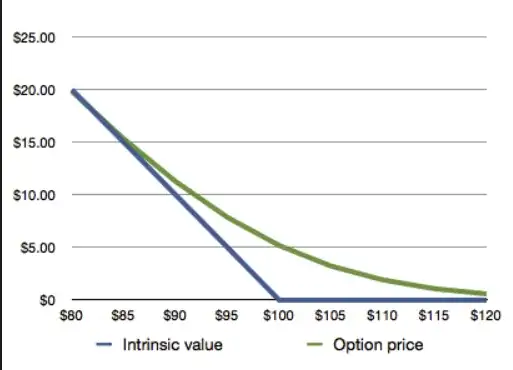
Now, the ITM value does not change 1:1 with the underlying and the Delta is slightly less than 1, and the OTM value is no longer zero and does change, so it's Delta is slightly greater than zero.
This effect is not directly because of "theta", but is because of the additional possibility of the option crossing the strike between now and expiry.
