How to compute the present value of a bond if the coupons aren't reinvested?

Question

We know that the computation of the present value of a bond assumes that the coupons paid are reinvested at the yield rate. But, what if I don't reinvest the coupons? How can I compute the present value?

For example:

100 Future value bond, 6% coupon paid semi-anually, the yield its 7%, and it matures in 10 years.

The computation would be:

FV: 100
Coupon: 100*0.06/2 = $3
Yield: 0.07/2 = 3.5%
Periods: 10*2 = 20

Which results in a PV = 92.8938. But this computation assumes that the coupons paid are reinvested at the yield rate. How can I do the same computation without the assumption of reinvesting the coupons?

Answer 1

It doesn't quite work that way.

Let me offer a counter example -

You buy my bond, $1000 face value, and it matures in 1/10 of a year. You get the $1000 back, along with a $10 coupon. A 1% return. 1.01^10 would be a 10.46% YTM. But, you say, "wait, what if I don't reinvest it for the 90% of the year remaining?" Do you want to claim I'm 'really' giving you a 1% return? Time matters.

Instead of thinking about the problem as "coupons are reinvested" consider "all returns are annualized rates". Not reinvesting the money is on you, it doesn't and I'd say 'can't' change the yield.

Answer 2

The semi-annual yield-to-maturity is 3.5% . The semi-annual coupon amount is 3 . And the bond redemption price is 100 with 20 semi-annual coupons remaining. Without compounding, that's a bond price of 94.12 as:

x/y = 3.5 * 20 / 100 ......... (Here the value of 100 just converts from percentage to decimal)

x = 0.7y

x + y = (3 * 20) + 100 .......... (Here the value of 100 is the redemption value)

0.7y + y = (3 * 20) + 100

1.7y = (3 * 20) + 100

1.7y = 160

y = 94.12

http://www.kbhscape.com/bond.htm

A simple logic, not really requiring algorithm, will prove the result:

100 - 94.12 = 5.88 as redemption price minus current price

5.88 / 10 years = 0.588

6 + 0.588 = 6.588 as annual coupon plus annual non-cash value

6.588 / 94.12 = 7% annual yield-to-maturity .

Answer 3

JTP is correct, but let me explain it another way:

What is "present value"? Is the the value today of cash flows in the future. To calculate the present value, one needs an appropriate "discount rate". This can be the rate at which you would need to borrow money to purchase the investment, or a "risk free" interest rate like from US Treasuries, or some other "required:" rate of return.

In your example, a "yield" is given to you. But what does that yield mean? It's the interest rate at which, given the market price, you could invest money and end up with the same value in the end as the investment.

For a bond, the assumption when calculating yield is that you are reinvesting the coupons at the same rate, and that rate is calculated iteratively.

A possibly better explanation of "yield" is at what fixed interest rate could I borrow/invest the cash flows to end up with the same amount at the end of the investment? So the assumption built into the concept of yield is that the coupons are "invested" at that rate. You don't have to invest them, but the price of the bond would be equivalent to investing them at that rate.

So it's not enough to just ask for a price "assuming coupons are not reinvested". The yield that you have includes that assumption. If you want a different price, you'd need to include a different yield that did not make that assumption. Then you'd discount the coupons and redemption at that rate to get a new PV.

If you want the yield that corresponds to that same price but coupons are not reinvested, you would just take the present value of all coupons and the redemption as if you get them at maturity. That calculation would be:

r = (100/P + n*c)^(1/n) - 1

Where n is the number of years to maturity and c is the annual coupon rate.

Answer 4

There is no reinvestment assumption in your calculation and in computing yield to maturity (YTM). All you have is 20 payments that you discount with the YTM.

In your case, you have 19 times a cashflow of 3, and a single cashflow of 103 at the end. These cashflows you discount with the computed YTM to get to the market value (or net present value / NPV) of the bond.

In Julia this could be computed like this (ignoring all details like day-count, leap years etc).

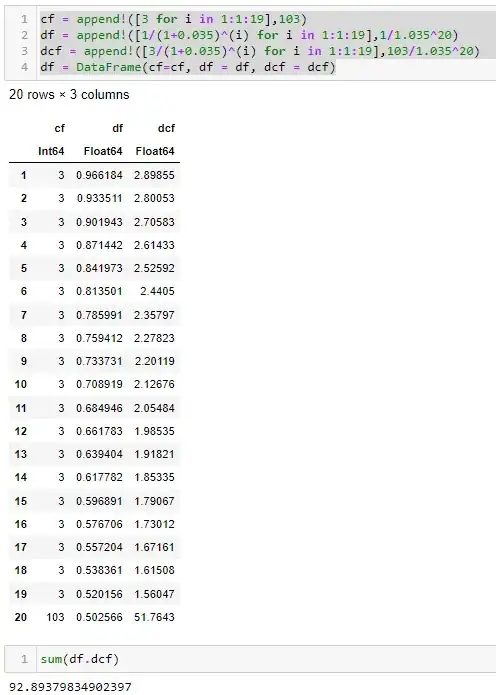
cf = append!([3 for i in 1:1:19],103)
df = append!([1/(1+0.035)^(i) for i in 1:1:19],1/1.035^20)
dcf = append!([3/(1+0.035)^(i) for i in 1:1:19],103/1.035^20)
df = DataFrame(cf=cf, df = df, dcf = dcf) 

There is no need to follow the code logic. The dataframe below shows the result. The first column (cf) represents the undiscounted cashflows. The second, (df), are the discount factors, and the third, (dcf), stand for the discounted cashflows.

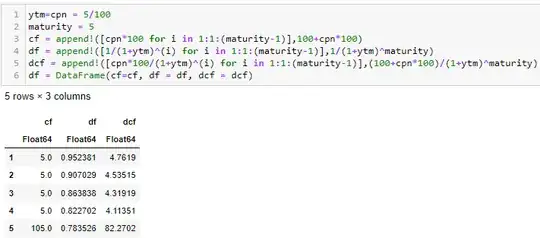
In this formula, there is nothing happening with all the coupon payments after they are received. Put differently, a 5% bond annual fixed rate bond simply pays a 5% coupon rate every year. If YTM is also 5% it is priced at par. Yet, if your bond has a maturity date in 5 years, you do not get 100*(1.05)^5 ~ 127,63 but simply 5*5+100 = 125 from the bond (see example below).

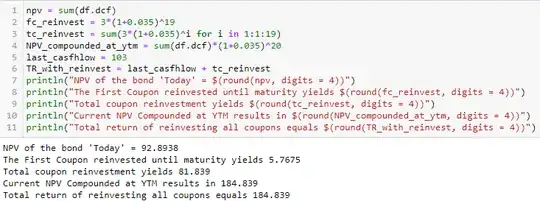
The confusion that many people have is that it is assumed that you get 127,63. However, this is not the case with a bond as you would have to compute the investment of every single coupon separately to get to this value. So for the first payment in your example, you would have 19 periods with compounding, which would yield an additional 3*(1+0.035)^19 ~ 5.77 in your example. Summing this for all 19 periods (the last coupon is only paid at the end), you add ~81.84 to your gain, and get a total of 184.84 as shown below with 100*(1.035)^20.

The example with 5% for 5 years looks as follows:

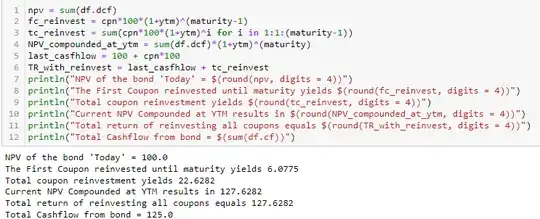
Long story short, the YTM has no reinvestment assumption and the NPV of the bond is computed without this reinvestment assumption because all it does is to discount the payments of the bond.