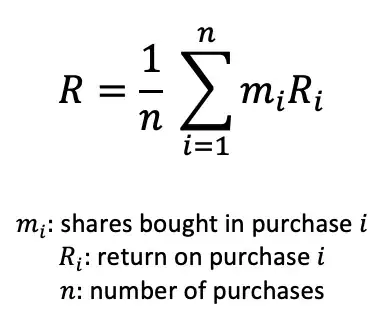2

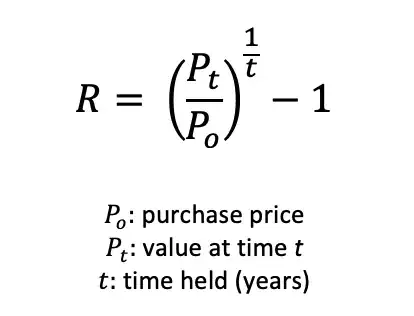
The annual rate of return on an investment can be calculated as CAGR of individual investment

And the top response to this question suggests that the return on a portfolio of such purchases is simply the weighted average of returns on individual transactions, where the weighting coefficient is the number of shares bought:

CAGR across portfolio of purchases

However, by this definition, it seems like the calculated portfolio return can be positive, despite losing money.

Consider the following example: I purchase two shares of stock, one for $100 and one for $10, and sell both for $50, the first held for 1 year and the second held for 0.5 years.

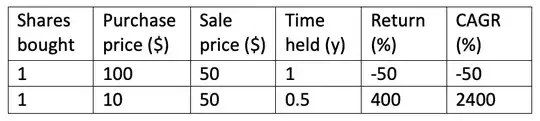
So I've spent $110 and received $100, but the calculated return is +1175% [ (-50% + 2400%)/2 ].

What am I doing wrong?

Michael Boles
  • 123
  • 4

1 Answers1

1

1st equation

R = (Pt/Po)^(1/t) - 1

annualised returns for shares 1 & 2 are

r1 = (50/100) - 1 = -50 %

r2 = (50/10)^(1/0.5) - 1 = 2400 %

2nd equation

R = Sum[mi*Ri]/n

Calculating half-year returns corresponding to the holding periods:

"weighted average of returns on individual transactions" for each half-year

hr1 = (100*(1 + r1)^(1/2) + 10*(1 + r2)^(1/2))/110 - 1 = 9.73698 %

hr2 = (1 + r1)^(1/2) - 1 = -29.2893 %

giving the return over the year as

(1 + hr1)*(1 + hr2) - 1 = -22.4042 %
Chris Degnen
  • 10,107
  • 1
  • 21
  • 36