20% APR means only 10% interest? (UK)

Question

I am trying to get better grasp of what the APR figure means, so this example is purely hypothetical.

I have entered a loan of £100,000 into an APR calculator on MoneySuperMarket with a 20% APR for the term of exactly one year. I think quite logically I would expect that the annual rate of 20% to mean around £20,000 paid in interest and fees throughout the year. However, it turns out that the actual cost is only a little more than half of this amount, at £10,228.

Why is the APR not a good prediction of the total cost in this example? Am I being naive in my understanding of what APR is supposed to represent?

The MoneySuperMarket is a UK website, so I expect it its APR calculation adheres to the requirements set by the British Financial Conduct Authority.

Answer 1

The APR is the amount of interest that you would pay if you held their money for a whole year. If you borrowed the £100,000 for a year, didn’t pay anything until the end of the year, and then paid it all off, then you would indeed be paying 20%, or £20,000 interest. However, since you are making payments, each month that goes by the interest charges decrease as you pay more of the loan off.

In the first month when you make your payment of £9,185.68, you are charged interest on the entire amount of your loan. The charge is 1/12 of the annual rate, or 1.67%, which would be £1,666.67. This means that £7,519.01 of your loan balance will be paid off with your first payment.

The next month, interest will only be charged on your remaining loan balance of £92,480.98. The interest charges the second month will be £1,541.34, and more of your payment will be going to pay off the loan balance than it did in the previous month.

By the time you get to your last payment, the interest charge will be quite small compared to the first month, as the loan balance will be almost paid off.

Answer 2

Your mistake is that in your calculation of interest ("10%") you divided the total amount of interest paid by the original amount you borrow. However, you don't pay interest for the original amount borrowed, but for the amount you are still borrowing during the time interval for which the interest is due (e.g. every month).

And since the system assumes constant monthly payments, your amount of principal still owed is constantly going down. E.g. after half a year you will have returned almost half of it, and the amount of interest adjusts accordingly.

Answer 3

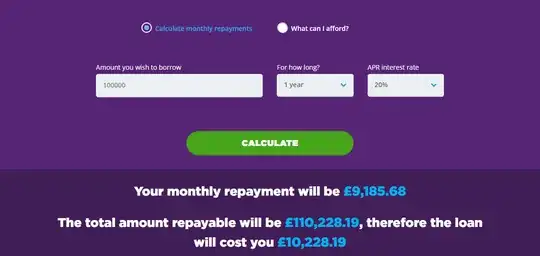
When you take a loan, there will be some interest rate in percent in your contract, and there will be some more or less "interesting" (or confusing, or misleading) rules how the interest payments are to be calculated. These rules would make it possible to give you a deal that is worse than it looks. Or much worse than it looks.

That's why APR was invented. APR takes into account the loan and all the payments that are made, and calculates a fair and mathematically sound interest rate. No matter what tricks the company giving the loan tries to use, APR lets you compare loans. A loan with 20% APR is a better deal than one with 21% APR, and worse than 19% APR and so on.

In your case, if you take a loan for one year, paid back in equal monthly payments, and the total payment is £110,228, so your interest payments are 10.228% of the original loans, then a fairly and mathematical sound calculation gives you 20% APR. The reason for the huge difference is that you owed £100,000 in the first month, but less than £10,000 in the last month, so you ought to pay 20% of £100,000 interest in the first month (divided by 12, obviously) but only 20% of £10,000 interest in the last month (again divided by 12).

Actually, I was present when a relative tried to get a loan for a car. (A few years ago, when interest rate was a lot higher). 5 years, 10%. That's what they said, that's what she would have signed. I checked the monthly payments, and it meant £12,000 were paid back for an £8,000 loan. Which meant the interest payment was 10% per year of the original loan. The APR was close to 20%, which they conveniently forgot to mention. I stopped the deal, and should have called Trading Standards. Thieving scumbags. They tried to scam her out of about £2,500.

Whenever you try to get a loan, insist on getting the APR in writing, and that's the real number that counts. Since giving the correct APR is a legal requirement in most countries, giving an incorrectly calculated APR will get them into deep legal trouble. Not if it's 20.1% vs. 20%, but if it's 20.1% vs. 10%.