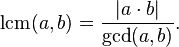4

I reinstalled the timing chain on my V6 Tacoma as per the Toyota official spec and the Haynes manual. I made sure that the marker notches on the intake camshaft sprockets line up to the marks on the cam bearings, per the spec. Then I turned the crank so that the marker on the crank sprocket is at 9 o'clock and then I mounted the chain so that the corresponding marker link straddles that crank sprocket marker and the other two marker links go over the corresponding notches on the camshaft sprockets mentioned above. Then I released the tensioner plunger.

However, when I turned the crank to make one full cycle of the chain and when the three marker links on the chain were in the same exact position they were in when I installed the chain, I noticed that the sprockets were not in the starting position.

I think this is as designed but I just wanted to check. Here is why:

I counted the number of links total on the chain and there are 87 wide links and consequently 87 narrow links that connect them. That is 174 holes that straddle cogs on the sprockets that transfer torque. The crank sprocket has 18 cogs and each intake camshaft sprocket has 36.

So in one full cycle of the chain, the crank sprocket turns 9.66 cycles (174/18) and each camshaft sprocket turns half that many, 4.83 cycles (174/36), as it has twice as many cogs. So when the single yellow marker on the chain that was initially lined up with the sprocket dot makes one full revolution, the crank will have turned 9 full cycles and 2/3 of a cycle so the sprocket dot will be exactly at 5 o'clock and not the original 9 o'clock (9 o'clock + 240 deg = 5 o'clock). Similar applies with different numbers for the two camshaft intake sprockets.

If my reasoning is correct, the lowest common denominator of 36 (which includes 18) and 174 is 1044, which means that it takes 6 revolutions of the chain (1044 / 174) or 58 turns of the crankshaft (1044 / 18) to line them all up again. The crank sprocket marker will be aligned with the yellow link on the chain after only 3 chain revolutions (as LCD of 18 and 174 is 522, 3 x 174) but the camshafts won't be aligned until that many more because they have twice as many cogs as the driving sprocket.

I was originally expecting that the number of holes on the chain would be exactly divisible by the number of cogs on both sprocket sizes so that each revolution of the chain would position each sprocket in exactly the same position (e.g. if there were 180 links/holes on the chain). But that is obviously not the case if my analysis is correct. I am posting here to get either an affirmation or negation of my analysis. Essentially, is it common that the number of links on a chain is not divisible by the number of cogs on sprockets, which necessitates several chain revolutions in order to line up to the initial state?

amphibient
  • 6,777
  • 42
  • 102
  • 139

1 Answers1

8

Yes, it is by design

... because it helps to equalize wear across the sprocket teeth and chain links.

Here's why

I had originally shared a link in the comments which presents the formula to calculate what's known as hunting tooth frequency. Mesh rate aside, this is governed by the the number of teeth in the sprocket and chain, a and b respectively:

gcd(a,b) / ( a * b )  // gcd = greatest common divisor

But mathematically, this is just a fancy rehash of the lowest common multiple of a and b:

gcd and lcm relation

So by choosing a and b such that the LCM is high, one can better distribute the wear across the sprocket teeth and chain links by allowing for more chain travel before a given sprocket tooth and chain link mesh together again.

This becomes important if a tooth gets chipped or damaged, or if one of the links in the chain causes undue wear due to (for example) manufacturing variation.

Here is a list of LCM's for your example:

lcm(36,80) = 720
lcm(36,81) = 324
lcm(36,82) = 1476
lcm(36,83) = 2988
lcm(36,84) = 252
lcm(36,85) = 3060
lcm(36,86) = 1548
lcm(36,87) = 1044
lcm(36,88) = 792
lcm(36,89) = 3204
lcm(36,90) = 180

So if the chain had 90 links instead of 87, the hunting frequency would be 1044 / 180 = 5.8x higher.

For the same reason, it would be better to have 85 links in the chain instead of 87 (roughly 3x longer before a bad tooth and link make contact again).

One might ask why Toyota, in their infinite wisdom, didn't choose 85 links instead of 87. There can be many reasons for this, including geometrical considerations, acceptable chain stress and the overwhelming pressure to follow standards.

Zaid
  • 39,276
  • 50
  • 151
  • 294