Bandpass vs. Resonance

Question

To pass a certain frequency, you can either have a resonant LC or a bandpass filter made from 2 capacitors and 2 resistors (a high pass and low pass filter put back to back. What is the difference between these two circuits, and is there an advantage of one over the other?

Answer 1

An LC filter is superior to using RC low and high pass filters for several reasons. One, it will provide a 12 dB/octave rolloff on both sides of the desired frequency while a single RC filter can only provide a 6 dB/octave rolloff. Two, it will automatically provide a symmetrical response around its center frequency while the 2 RC filters must have matching components to achieve this. Three, the Q of an LC bandpass filter, if a good quality inductor is used, will exceed that possible with RC filters. However, LC filters can be physically large depending on the frequency. Also inductors are subject to non-linear effects if the signal levels are large.

Answer 2

Assume you have two RC filters cascaded (with an op-amp buffer to remove the interaction between the two filters), one high-pass and one low-pass with the same corner frequency and unity gain buffer:

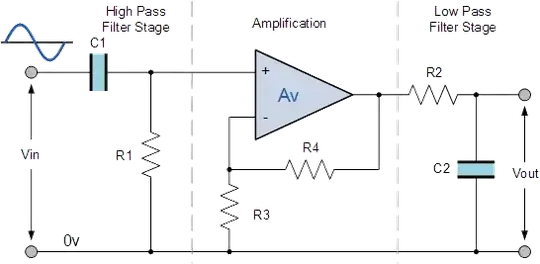
The overall transfer function is:

$$H(s) = \dfrac{\frac{s}{RC}}{s + \frac{1}{RC}} \dfrac{1}{s + \frac{1}{RC}} = \dfrac{1}{2}\dfrac{\frac{2s}{RC}}{s^2 + \frac{2s}{RC} + (\frac{1}{RC})^2}$$

By inspection, this filter has \$Q = \frac{1}{2}\$ and that's the highest Q one can get with this topology.

Now, assume you have a series RLC bandpass filter instead:

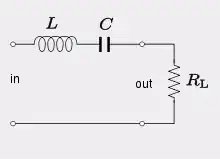
where $$H(s) = \dfrac{s\frac{R_L}{L}}{s^2 + s\frac{R_L}{L} + \frac{1}{LC}} $$

By inspection, this filter has \$Q = \frac{1}{R_L}\sqrt{\frac{L}{C}}\$ thus, the Q of this filter can be much higher than 1/2.

So, if you need a selective, high-Q filter, you would not want to use the RC HPF - LPF cascade.