LC Low Pass FIlter in Buck Converter

Question

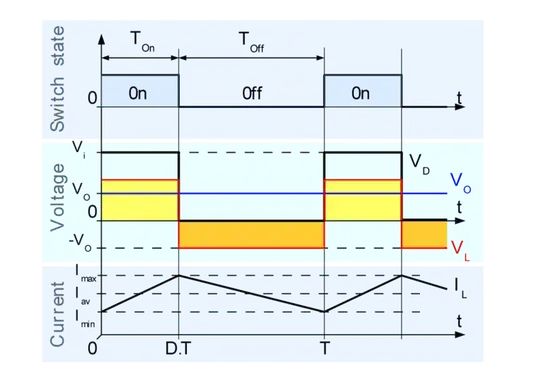
Hi In this circuit below: enter image description here

What role is the LC Low Pass filter playing?

The switch is switching ON-OFF alternatively, at a frequency which determines the Duty cycle, and we get an average output at the point before L. Now why do we need to hook up an LC Low Pass filter for that signal?

I did understand that L would prevent Sudden current change and C would prevent Voltage change, but what exactly is the role as a filter? And how does switching frequency effect that?

score 3 · Accepted Answer · answered Sep 07 '13 at 23:58

3

Assuming ideal components, if you did not have the loop and capacitor, you would get square wave.

Let us consider the simple case: 50% duty cycle, 10V. This is mathematically equivalent to

5V DC +
4/pi * sin(2pi*f*t) +
4/pi * sin(6pi*f*t)/3 +
4/pi * sin(10pi*f*t)/5 +
etc.

As you see, everything except the DC is not DC*, so if you put a lowpass filter on that signal, you get out 5V DC

To rephrase: You said that you know the capacitor is to maintain same voltage and the loop is to maintain same current - well that's what a DC lowpass filter does.

*I know, that sentence was written by Captain Obvious.

EDIT: If anybody wants to edit for layout, feel free.

answered Sep 07 '13 at 23:58

shieldfoss

420
1
4
10

1

Thanks! So if i understand this correctly, is the output part of switching a square wave, which is fed to the LC Circuit, and is made smooth? and is there somewhere, where i can read more about how that part is made smooth? – Sherby Sep 08 '13 at 00:05
1

@Sherby Not without getting into filter theory, I'm afraid. – shieldfoss Sep 08 '13 at 00:09
3

@Sherby I should add: It's not ACTUALLY smooth. If you put a sufficiently good oscilloscope on a buck or boost converter, you will find that it is NOT DC, it is just approximately DC. In reality, it is DC plus a slight ripple; this ripple will have a frequency that fits with the characteristics of the LC filter you have built into your circuit. – shieldfoss Sep 08 '13 at 00:15

score 3 · Answer 2 · answered Sep 08 '13 at 01:15

The average voltage at point L is a pulsating square wave of amplitude \$V_g\$.

The inductor will limit the current flowing by the usual inductor formula:

\$ V_L = L \dfrac{di}{dt} \$

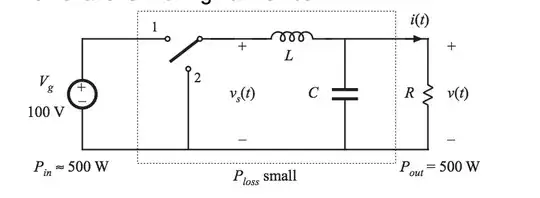
When the switch is in position 1, current ramps up in the inductor:

\$ V_L = V_g - v(t) \$

\$ V_g - v(t) = L \dfrac{di}{dt} \$

\$ di = \dfrac{[V_g - v(t)] \cdot dt}{L} \$

When the switch is in position 2, current ramps down in the inductor:

\$ V_L = 0 - v(t) \$

\$ -v(t) = L \dfrac{di}{dt} \$

\$ di = \dfrac{-v(t) \cdot dt}{L} \$

The net result of this is a triangular current waveform. Since the capacitor is constantly being charged by the inductor, its voltage will be the average of the pulsating square wave with triangular ripple voltage induced across its ESR by the triangular current waveform coming from the inductor.

The energy storage of the inductor is what allows the converter to work; in fact, inductive energy storage is how the majority of PWM-based switching converters are able to do what they do.

enter image description here

LC Low Pass FIlter in Buck Converter

2 Answers2