2

I am trying to solve a question in a text book of resistive circuit using KVL. The circuit is as follows :

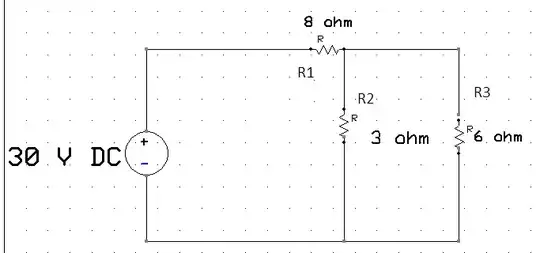
enter image description here

I have to calculate the voltage through each resistor. What I have got is:

  • V1 = 24V
  • V2 = 18V
  • V3 = 18V
  • I1 = -3A
  • I2 = 3A

The actual values are (on the answers sheet)

  • V1 = 24v
  • V2 = 6V
  • V3 = 6V

An answer with proper calculations will be highly appreciated.

PeterJ
  • 17,201
  • 37
  • 57
  • 91
Abdul Zahid
  • 21
  • 1

2 Answers2

1

In Nodal analysis (KCL),

Kirchhoff's Current Law implies that the sum of currents going in equal to the sum of currents going out. $$\Sigma_{k=1}^n {I}_{in} = I_{out}$$

A.) So you have two ways of going at it either

  1. assume all currents are going in to a node. Then construct an equation in which that the the addition of all currents is equal to zero
  2. intuitively decide in each branch if the current is going out, or going in. Then construct an equation where the left-hand side is the addition of currents going into the node, and right-hand side is the addition of the currents going out (or vice-versa)

B.) There exists a useful equation for each node in which more than two branches meet. So in this case there is 1 good equations. For each node i'd recommend assigning a variable (like Va for the one between all resistors)

We subtract the voltage at the tail of the direction of current to that of the head it would be as follows

(going into node) $$I_{1} = (30-Va)/8$$ (going out of node) $$I_{2} = Va/3$$ (going out of node) $$I_{3} = Va/6$$
note: current subscript correspond to resistor subscript $$I_{1} = I_{2} + I_{3}$$ $$(30-Va)/8 = Va/3 + Va/6$$

Simplify this and you notice Va = 6, thus the book answers are correct.

Iancovici
  • 2,246
  • 17
  • 28
0

In nodal analysis, one solves for the node voltages. There are 3 nodes in your circuit one of which is the datum or zero node. In this circuit, the zero node should be the one the negative end of the voltage source connects to.

The voltage at the node that the positive end of the voltage source connects is 30V by virtue of the voltage source connected there.

Thus, the only unknown node voltage is the node the three resistors connect to. Let's label that node voltage \$V_A\$.

Then, by KVL, the resistor voltages are:

\$V_1 = 30V - V_A\$

\$V_2 = V_3 = V_A\$

So, how to solve for \$V_A\$?

Write a KCL equation at that node:

\$\dfrac{V_1}{R_1} = \dfrac{V_2}{R_2} + \dfrac{V_3}{R_3}\$

Substituting the equations from the first part into the equation above yields:

\$\dfrac{30V - V_A}{R_1} = V_A \left( \dfrac{1}{R_2} + \dfrac{1}{R_3} \right)\$

Now, solve for \$V_A\$ and then for the resistor voltages. You'll find that the answers match the answer sheet.

Alfred Centauri
  • 26,630
  • 1
  • 25
  • 63