I'm working on a design that involves a lot of max functions (and max functions as arguments to other max functions).
In an effort to simplify the hardware design I was wondering how max is implemented in hardware?
Mathematically, Max(a,b) can be represented as [(a + b) + abs(b - a)]/2.
Is this how its implemented in hardware? (i.e. in stages; addition, bit shift division, etc.)
If so, how is the absolute of the difference calculated?
A very simple approach would be to implement (a>b)?a:b. a>b can be implemented by starting at the left and check each bit pair of (a,b):
When you know which one is the highest you can select that one by a 2N->N mux.
With some clever tricking the checking of the bit pairs can be combined with the muxer for the same bit pair.
Lets look at the algorithm in the question:
[(a + b) + abs(b - a)]/2
This has an addition and subtraction stages which are then fed to a second stage addition. The divide by 2 is trivial in hardware, it can be done by removing the LSB. However the two-stage full-adder/subtractor is pretty slow and gate-intensive, especially if you are cascading multiple caparisons like you are.
Building off of Wouter van Ooijen's answer, the generalized structure is a digital comparator feeding the select signal of a mux:
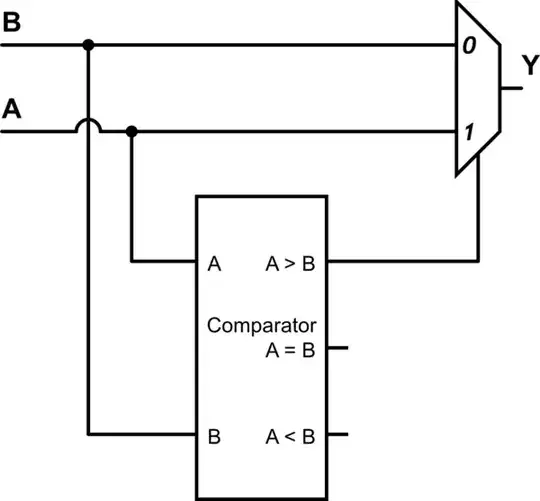
simulate this circuit – Schematic created using CircuitLab
The above schematic is for:
(A > B) ? A : B
but notice that it can be easily reconfigured for any comparison between the two inputs by making different logical connections between the comparator outputs and the mux select.
So if we know how to formulate the three outputs from the comparator, we can implement any comparison in hardware. Comparator logic is well described here. To optimize the hardware, we would just remove the logic driving the unused comparator outputs.
But in the end, if its going to hardware, it has to go through synthesis. So you shouldn't obsess over which gate-level scheme is optimal. Instead, optimize your code and algorithms so that you at least are not forcing the synthesizer to produce an inefficient result. "With some clever tricking the checking of the bit pairs can be combined with the muxer for the same bit pair," and the easiest way to perform this optimization is with synthesis.
If you really want to build a specialized circuit to compute the max, you can start with a basic block with the following equations:
$$\begin{eqnarray} E_{i,out} &\leftarrow& E_{i,in} \wedge \neg (a_i \oplus b_i) \\ L_{i,out} &\leftarrow& (\neg E_{i,in} \wedge L_{i,in})\vee (E_{i,in} \wedge a_i \wedge \neg b_i)\\ r_i &\leftarrow& (\neg E_{i,in} \wedge ((L_{i,in} \wedge a_i) \vee (\neg L_{i,in} \wedge b_i))) \vee (E_{i,in} \wedge (a_i \vee b_i)) \end{eqnarray}$$
and then connect them with the most significant digit feeding the next one. The critical part goes from the MSB to the LSB while circuit based on substraction will at best have a critical path going from the LSB to the MSB then back to the LSB.
It is the equivalent of a carry-ripple adder. If you are interested you can build the equivalent to carry-save or carry-select adders.
(\$E\$ means equal until here, and \$L\$ has a meaning only if \$\neg E\$ and means select \$a\$)
