Mass paralled resistors for better tolerance

Question

I hope this doesn't get people's eye rolling as a very rudimentary question...

Here goes. I need a very, very precise resistor divider, say a 1/11 ratio. It doesn't really matter the ratio chosen. Just as long as it is known & very precise. It so follows both R1 & R2 needs to be in very, very tight tolerances. My approach is to simply parallel SMD resistors so it adds up R1 & also parallel resistors into R2.

Starting off:

$$R(1 + t_j) = R + R t_j$$ where \$R\$ is the ideal value of the resistor & \$R t_j\$ is the tolerance.

---

By some light math we should be able to show parallel resistors: $$(\sum_{j=1} ^n (R(1 + t_j))^{-1})^{-1}$$

Let \$\bar t \$ exist & be the average tolerance: $$\Rightarrow (\sum_{j=1} ^n (R(1 + \bar t))^{-1})^{-1}$$

$$\Rightarrow (\frac{1}{R(1 + \bar t)} \sum_{j=1} ^n 1)^{-1}$$

$$\Rightarrow (\frac{n}{R(1 + \bar t)})^{-1}$$

$$\frac{R}{n} + \frac{R \bar t}{n}$$

Parallelizing narrows it's tolerance with \$\frac{R \bar t}{n}\$, even if it lowers it's ideal resistance of \$\frac{R}{n}\$.

So, for example, having made my R1 with (n = 16) 1k ohm resistors with 0.05% individual tolerances, the total narrower tolerance is 0.003125%. For R2, if I used (n = 16) 10k ohm resistors with, also, 0.05% tolerance, the narrower tolerance should be, likewise 0.003125%.

Then, I took a handful (not all, but a handful) of these SMD 1k & 10k ohm resistors & individually measured them. For the 1k ohm, all measured 1.002k ohm in the 2k range of my multimeter. As for the 10k ohm, all measured 10.00k ohm in the 200k range of my multimeter. I guess the tolerance ranges are hiding behind the resolution of my multimeter's ranges.

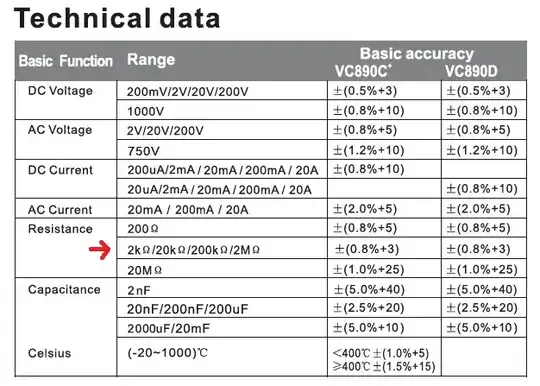
Parallelizing 16 SMD resistors via reflowing them into the PCB, I was expecting 62.625 ohms (1.002k ohm/16) & 625 ohms (10.00k ohm/16) both with tolerances of 0.003125%, below the resolution of my multimeter. I'm sure. So it's possible it was accuracy issues when I measured 63.4 ohms & 631 ohms. Although, these are deviations of 1.238% (|63.4 - 62.625|/62.625) & 0.96% (|631 - 625|/625). When I looked up the accuracy specs off the multimeter in question (I must've lost the manual it came with), those are above the multimeter's accuracy limits of ±0.8% + 3.

Or, perhaps I'm misreading this. What's 3 in "±0.8% + 3"?

---

Btw, in series:

$$\sum_{j=1} ^n R(1 + t_j)$$ $$\Rightarrow nR + \sum_{j=1} ^n t_j$$ Averaging, let: \$\bar t = \frac{\sum_{j=1} ^n t_j}{n} \Rightarrow \sum_{j=1} ^n t_j = n \bar t \$ $$nR + nR \bar t$$

Answer 1

You need to do a four-wire resistance measurement if you want real precision. A cheap multimeter isn't going to do the job.

I think your approach of using many resistors to average out the tolerance is flawed. It would handle random variation between individual resistors but wouldn't help you with variation between manufacturing batches. For high precision, you would normally do trimming or calibration. For trimming, you could consider adding tiny resistors in series with your main resistor(s) to adjust the total resistance. Calibration would be done on whatever overall result your system is producing.

You'll also need to keep temperature variation in mind. Even with a (pretty good) 50 ppm/°C temperature coefficient, a 10°C rise in temperature will change a resistance by 0.05%. So make sure that both of your resistances are built from the same kinds of resistors and see the same temperature.

Answer 2

Resistors have specs. Some known. Some unknown.

You generally don't know the distribution of the tolerance of the single resistor, so you cannot guess if multiple resistors connected together have any better distribution or not.

Resistors also change resistance when they age, or when you solder them, or based on their temperature, so it really does not matter much, if you buy resistors with 0.05% tolerance, as that's the initial tolerance, measured under some specific operating conditions.

Sometimes, in sensitive circuits, you need to take other things into account, such as moisture changes, and Seebeck effect of the solder joint.

It seems like you are aiming for a precise voltage divider. Generally the resistors are not the limiting factor but what you do with them.

However, precision resistor networks do exist and can be custom ordered. Sometimes even standard resistor networks are useful, they may have 1% tolerance for the resistances, but as the resistors are manufactured in the same process, the individual resistors may have values very close to each other.

Answer 3

There are benefits in what is proposed even if the tolerances are not normally distributed which is likely. Same value resistors should have the same tempco and they have the same self heat because the terminal voltages are the same.

Answer 4

So, for example, having made my R1 with (n = 16) 1k ohm resistors with 0.05% individual tolerances, the total narrower tolerance is 0.003125%. For R2, if I used (n = 16) 10k ohm resistors with, also, 0.05% tolerance, the narrower tolerance should be, likewise 0.003125%.

@MathKeepsMeBusy How can deviation shrink, but the tolerance stay the same? Show more math please

A 10 k\$\Omega\$ resistor with a 1% tolerance can have any value between 9.9 k\$\Omega\$ and 10.1 k\$\Omega\$.

10 of such resistors in parallel will have a combined resistance with a value anywhere between 9.9/10 = 990 \$\Omega\$ and 10.1/10 = 1.01 k\$\Omega\$

The nominal value of the combined resistance is 1 k\$\Omega\$. The absolute tolerance has indeed dropped from 100 \$\Omega\$ to 10 \$\Omega\$. But the tolerance as a percentage of the nominal resistance is still 10\$\Omega\$/1000\$\Omega\$ = 1%.