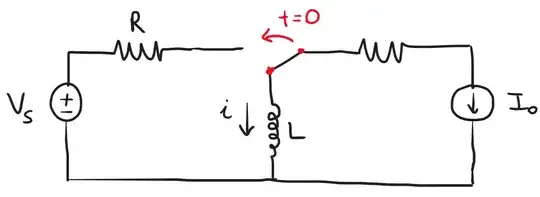
The unknown constants present in the homogeneous solution must be determined when the initial conditions for \$t=0_+\$ are satisfied by the complete response \$i(t)=i_p(t)+i_h(t)\$.
Your particular solution \$i_p(t)=\frac{V_s}{R}\$ is correct (also called forced response). Note that, although there are numerous ways to find the homogeneous solution \$i_h(t)\$ (also called natural response or complementar one), it's still possible to modify your method, just leaving the calculation of unknow constant for later:
$$\int_{}{}\frac{di}{i} = -\int{}{}\frac{R}{L} dt$$
$$\ln(i_h) =-\frac{R}{L}t +\mathbb{C}$$
$$i_h(t)=e^{-\frac{R}{L}t+\mathbb{C}}$$
$$i_h(t)=e^{-\frac{R}{L}t}e^\mathbb{C}$$
Making \$K=e^\mathbb{C}\$:
$$i_h(t)=Ke^{-\frac{R}{L}t}$$
Then, the complete solution is:
$$i(t)=i_p(t)+i_h(t)$$
Or:
$$i(t) = \frac{V_s}{R} + Ke^{^-\frac{R}{L}t}$$
As I mentioned earlier, the constant \$K\$ is determined when the initial conditions (\$t=0_+\$) are satisfied by the complete solution:
$$i(0_+)=\frac{V_s}{R} + K=-I_0$$
$$K=-\frac{V_s}{R}-I_0$$
Finally:
$$i(t)=\frac{V_s}{R} - \left( \frac{V_s}{R}+I_0 \right) e^{-\frac{R}{L}t}$$
Valid for \$ 0 \lt t \leqslant \infty \$.
----------- Detailed explanation --------------
There are several ways to express the complete response of a system, typically given by the sum of two separate responses. The best known are:
(1) Natural (homogeneous) solution + Forced (particular) Solution.
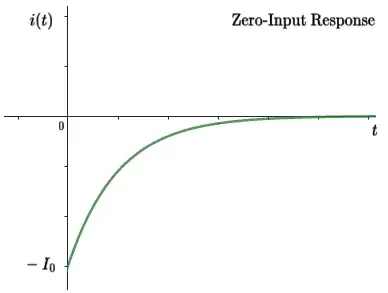
(2) Zero-State Response + Zero-Input Response.
(3) Transient Response + Steady-State Response.
For a more detailed discussion, see my other answer (related with the subject) here:
https://electronics.stackexchange.com/a/695628/22676
Your intention was to use the form (1), which is more used by math people, but it is not widely used in modern electrical engineering, as it is based on initial conditions \$t=0_+\$. Currently, form (2), which is based on initial conditions \$t=0_-\$, is preferred, since it conforms to the solution given by the unilateral Laplace Transform (with initial conditions \$t=0_-\$). Also note that, for \$t=0_-\$, the input did not yet exist. Even so, I tried to give an answer that adapted your solution.
In order to get the complete solution it's enough to use the method of separation of variables:
$$L\frac{di}{dt}+Ri=V_s$$
$$\frac{diL}{V_s-Ri}=dt$$
I'm going to use initial conditions in \$t=0_-\$. Notice that, in this case, \$i(0_-)=i(0_+)=-I_0\$:
$$L\int_{i(0_-)}^{i}\frac{d \varsigma}{V_s-R \varsigma}=\int_{0}^{t}d \tau$$
$$-\frac{L}{R} \left [ \ln \left ( \left | V_s-R \varsigma \right| \right ) \right ]^{i}_{i(0_-)}= t$$
$$-\frac{L}{R} \left [ \ln (V_s-Ri) - \ln(V_s-Ri(0_-)) \right ]= t$$
$$\ln(\frac{V_s-Ri}{V_s-Ri(0_-)})=-\frac{R}{L}t$$
So, when replacing \$i(0_-)=-I_0\$, we can get the form (1) as shown below. Remember that, the natural solution (or homogeneous one) brings together the characteristic modes (system poles).
$$i(t)=\underbrace{\frac{V_s}{R}}_{Forced \space solution} - \underbrace{\left( \frac{V_s}{R}+I_0 \right) e^{-\frac{R}{L}t}}_{Natural \space solution}$$
Valid for \$ 0 \lt t \leqslant \infty \$.
Through a simple algebric handling, we can get the form (2):
$$i(t)=\underbrace{\frac{V_s}{R}\left ( 1-e^{-\frac{R}{L}t} \right)}_{Zero-State \space resp.} - \underbrace{I_0 e^{-\frac{R}{L}t}}_{Zero-Input \space resp.}$$
Valid for \$ 0 \lt t \leqslant \infty \$.
In summary: You ended up mixing the two types of solutions. In fact, your original method
$$\int_{i(0)}^{i_h} \frac{di}{i} = -\int_{0}^{t} \frac{R}{L} dt$$
is related to get the Zero-Input Response, rather than the homogeneous solution (remember the difference between initial conditions \$t=0_-\$ and \$t=0_+\$). Is similar to separation of variables solution which I've presented above - just making \$V_s=0\$.
------ RESPONSE TO LAST QUESTIONS IN COMMENTS (Figure) -------
1. With no use of Laplace transform, is preferable to get the complete response (which can be separated in a sum of different responses later) through the Method of Separation of variables according my answer (for systems with order higher than one, that is not applicable). Of course, there are other methods presented in literature as choosing a linear combination of exponentials from a predefined table along unknown constants.
2. Yes, you can still use your method to find the Zero-Input response. In this case, is more convenient to choose the lower limit of integral as a generic \$i(0_-)\$, instead of \$-I_0\$ and only replace it later (with the negative value). In this manner, you won't have problems with signs.
I think the reason lies in the absolute value involved with the \$ln\$ (natural log) function which results from integrating the \$1/i\$ (hyperbola function) from a higher value in magnitude to a lower in magnitude. See the figure. The integration "does not know" the difference (if the initial current and the final one are both \$> 0\$ or \$< 0\$). Notice that both areas are equal in magnitude and also negative in sign.
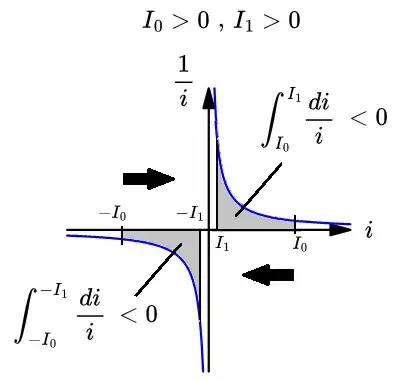
Otherwise, if you still to want use the \$-I_0\$ from the beginning of integration, you should fix the sign at the end for yourself. Example:
$$\int_{-I_0}^{i}\frac{d \varsigma}{\varsigma}=-\frac{R}{L}\int_{0}^{t}d \tau$$
$$\left [ \ln{ \left | \varsigma \right | } \right ]_{-I_0}^{i}= -\frac{R}{L}t$$
$$\ln(|i|) - \ln(|-I_0|) =-\frac{R}{L}t$$
$$\ln \left ( \frac{|i|}{|-I_0|} \right ) = -\frac{R}{L}t$$
$$ |i(t)|=|-I_0|e^{-\frac{R}{L}t} $$
Obviously, if you choose
$$ i(t)=I_0e^{-\frac{R}{L}t} $$
this expression does not correspond to your circuit. But, you know that the Zero-Input Response \$i(t)\$ is negative for any value of \$ t \ge 0\$. Then:
$$ i(t)=-I_0e^{-\frac{R}{L}t} $$