2

I'm completely new to electrical engineering. I came across KVL and my previous intuition about how voltage works broke down when coming across an example of KVL and parallel resistors.

Some background: My understanding of voltage is that it is the amount of energy needed to move an electrical charge across 2 points in the circuit.

I use the water analogy for the basis of my intuition for resistors. If you have water flowing through a pipe, a resistor is basically a narrowing of the pipe making it harder to move current through. AKA the larger the resistor the more energy needed to move current through.

So if we take an example like this my understanding breaks down:

Example circuit with parallel resistor

With the two resistors on the right, I would think that the larger resistor would have a greater voltage across it, but it's the same as the other parallel resistor according to KVL.

If you have a larger resistor, wouldn't you need more energy to move a charge through it? How could it be the same as the smaller resistor?

Clearly I'm missing something, probably a few things...Can someone make this make sense and provide an analogy or some kind of intuitive understanding?

Clueless
  • 43
  • 5
  • Try to think of voltage as the pressure of a fluid, current as the flow rate, and a resistor as a more or less thin piece of piping (that creates friction). – Jonathan S. Feb 25 '24 at 22:06
  • 2
    Honestly, I'm an electrical engineer, and the water analogy model just … confuses me. Maybe try understanding electricity without it, because: you seem to be doing quite well! Yes, voltage is the difference in energy per charge! And that's why there's less current flowing through the larger resistor, leading to less power (which is the product of voltage and current) being converted to heat by that resistor. I honestly can't find a coherent explanation based on water for this, I very quickly end up in situations where water pressure and flow just are way more complicated than, well, currents – Marcus Müller Feb 25 '24 at 22:16
  • 2
    …through resistors. I've been talking to many people about the water analogy, and many find it helpful for initial intuition, but some are like me and just never quite got the water model, although we all find linear electrical networks quite intuitive. It might just be that the water/pipe model isn't good for everyone (I maintain it's at most as easy as the actual thing, and you can't see how much water per second goes through a pipe or what pressure is on a container without a measurement devices either… So why teach A to teach B if A is at least as hard and intangible as B?) – Marcus Müller Feb 25 '24 at 22:17
  • 2
    @MarcusMüller Completely agree. Apparently when this analogy started, everyone was a professional plumber and knew what happens to water when you connect three pipes of different dimensions to a valve etc. I definitely don't. – pipe Feb 25 '24 at 22:49
  • @pipe what are your thoughts on nominative determinism? – vir Feb 25 '24 at 23:11
  • @vir My PCP's name is Promporn. I'll keep an eye out. ;) – periblepsis Feb 25 '24 at 23:31
  • Clueless, It's nice you colored the nodes of the circuit as you did. Handy. Think of each colored node as a solid bar of copper with an untold number of free electrons in an ocean. There simply cannot be any voltage differences in that solid copper bar. If there were any voltage difference at all, one place to another, then electrons would move accordingly, and instantly, such that there was no remaining difference anywhere in that sea. There just cannot be any voltage difference of any size for any time there. It just doesn't happen. It can't. Now, is just that much intuitive to you? – periblepsis Feb 26 '24 at 00:41
  • Clueless, You can kind of think of that ocean as having a sea level of sorts and there simply cannot be any differences in the level as it is, by definition, self-leveling. I'm wanting you to focus on this idea because if it makes sense to you and you can hold it in mind, then you must also see that there cannot be any voltage difference across those two resistors you mentioned. It's just not possible. So this means there is a contradiction in ideas here. If you accept my thought, then you must reject yours. They cannot be simultaneously true. So think about it for a moment. – periblepsis Feb 26 '24 at 00:44

2 Answers2

2

I'm with Marcus Muller on this. I can make the water analogy work, but learning the water system first then electronics means that you must do twice the work for the task at hand.

the larger the resistor the more energy needed to move [the same] current through.

I can form a corollory by saying "Less current will move through a larger resistor for the same energy

Rely on the basics, the fundamentals. There aren't that many.

  1. Elements in series must have (must have) the same the same current through them. Elements with greater resistance must have a greater voltage across them.
  2. Elements in parallel must have (must have) the same the same voltage across them. Elements with greater resistance must have a lower current through them.
  3. KVL: The voltages measured around a closed path (with consistent oriention along the path) must (must) add to zero.
  4. KCL: The sum of the currents measured entering a node must (must) equal the sum of the currents leaving the same node.
  5. Ohm's law. Resistance is the voltage across and element or combination divided by the current through the same element or combination.

Laplace impedance (once you know) allows the concepts to be used for capacitors and inductors as well.

Memorize these 5 concepts and trust them implicitly. As you learn more there are more defining relations, but these 5 will always be dependable. Items 1 to 4 work also for non-linear systems.

Practice writing equations that represent their meaning.

RussellH
  • 15,016
  • 2
  • 10
  • 38
1

Perhaps a revision of some of your statements is in order. You said:

My understanding of voltage is that it is the amount of energy needed to move an electrical charge across 2 points in the circuit.

Correct, but easy to misinterpret. The truth is that any voltage will eventually move a charge from one place in a circuit to another. What changes is the rate at which charges complete that journey.

the larger the resistor the more energy needed to move current through

Very misleading. Voltage is a measure of energy that a charge would have to lose on a complete journey through the resistance. That doesn't mean that you can't have quadrillions of charges moving only part way through it, losing only a small chunk of their energy.

Current is a measure of how many charges are entering or leaving the resistor each second, and is not to be confused with how many charges are completing the entire journey through the resistor. Probably no single charge will make the complete journey, unless you leave that current flowing for a long time.

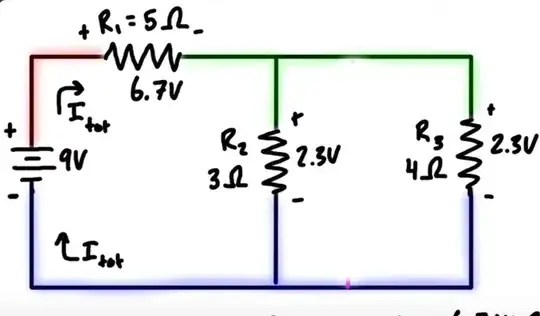
With the two resistors on the right, I would think that the larger resistor would have a greater voltage across it, but it's the same as the other parallel resistor according to KVL

The voltage across each resistor R2 and R3 is indeed the same according to KVL, but...

If you have a larger resistor, wouldn't you need more energy to move a charge through it? How could it be the same as the smaller resistor?

It is correct to say that with the same voltage across them, the difference between the potential energy of a charge found at one end of R2/R3, and the potential energy of a charge found at the other end, is the same. That is, in both cases, a charge that completes the journey via either resistor will have lost the same amount of energy after a complete journey through its respective resistor.

However, again it's not correct to say that any charge makes that complete journey. All else being equal (resistor dimensions, cross-section area, charge density etc), the average speed of individual charges through the 3Ω resistor will slightly greater than (by a factor of \$\frac{4}{3}\$) than the average speed of charges in the 4Ω resistor.

Consequently, more charges are entering the top of R2 each second (and leaving at the bottom), than are entering (and leaving) R3 each second. This is the definition of current: quantity of charge passing some point in one second.

It would be correct to say that after a long, long time, \$\frac{4}{3}\$ as many charges will have completed the journey through R2 compared to charges travelling through R3.

Instantaneously, that picture doesn't work, because in a tiny fraction of a second, no single charge has time to complete the journey. Yet current is still flowing, and is non-zero. I repeat, that's because there are quadrillions of charges travelling part-way, rather that just a few making it all the way through.

Your interpretation of voltage is correct, though, just don't forget that a charge that moves only, say, half way between two points of potential difference (half way through the resistor) will only lose half of its potential energy, but it still moved, and it still contributed to current! There's always another charge that started half-way, and made it out of the resistor!

Just extend that description of behaviour to quadrillions of charges, each moving only a tiny distance in each second, and you'll get a better picture of what's going on.

Simon Fitch
  • 34,939
  • 2
  • 17
  • 105
  • Thanks for this, I think my misunderstanding had to do with energy. After reading this post and googling I saw that energy = Power x Time and Power = Voltage x Current

    So the voltage for the parallel resistors can be the same because the lower value resistor leads to more power and less time while the higher value resistor leads to less power and more time, equaling out to the same potential energy over the respective resistors.

    And like many of the comments for this post mention, trying to relate it back to the water analogy makes it more confusing than it needs to be.

     – Clueless Feb 27 '24 at 15:48