Frequencies are inherently positive physical quantity.... what does it mean?

Question

While I was going through a digital signal processing course, I came to this problem where it says that "Frequencies are inherently positive physical quantity" - Digital Signal Processing by John G Proakis, Page 15. I didn't really get the intuitive idea. Can anyone explain this sentence a little bit or suggest some resources?

Answer 1

Frequency is how many times something happens every second. So it can't be "minus 5 times a second". However when you do actual signal processing, you'll see negative frequency on the graph too.

Answer 2

Frequency is related to time. Time in systems is only positive. For theoretical purposes you can consider time to be negative, but in the real world time is always positive

Answer 3

Consider a spinning disc. It can rotate clockwise or counter-clockwise. Clockwise angles \$\theta\$ are considered negative while counter-clockwise angles positive,

The angular velocity \$\omega\$ is the time rate of change (derivative) of the angular position. $$ \omega=\frac{d\theta(t)}{dt}\tag{equ 1} $$ which can be positive or negative.

If spinning at a constant rate (periodically) then the equation can be integrated over one rotation to show that: $$ \omega T=\pm 2\pi $$ where T is called the period of rotation.
\$2\pi\$ is positive or negative depending on whether the integration is clockwise, or counter-clockwise.

Since frequency is the inverse of period, \$f=\frac{1}{T}\$ then it is always positive as indicated by voltage Spike's answer.

So in the relation: $$ \omega = 2\pi f $$

should probably be written $$ \omega = \pm 2\pi f $$

When negative frequencies are plotted, they should be considered as angular (phase) velocities as in equ 1.

The angular velocity is sometimes, loosely, called the radian frequency which can be confusing on this point.

This discussion centres on the mechanical rotating disc, but the concepts are routinely applied in all areas of STEM, as well as DSP.

Answer 4

In common usage, frequency is an absolute magnitude, and thus positive. This is similar to how speed is positive regardless of travel direction.

• If you count the number of passing street lights to determine your speed, you always get a positive value.
• If you count the number of tick-tock sounds from your clock to determine its frequency, you always get a positive value.

However, this is just a matter of definition. To avoid confusion, the signed counterparts have their own names:

• If you define a positive direction of travel, and then make a U-turn, your velocity is negative.
• If you define a positive direction for your clock, and adjust the mechanism to run backwards, its signed frequency is negative.

Velocity finds most use in physics problems and rarely in day-to-day life. Signed frequency finds most use in signal processing and rarely in day-to-day electronics.

Answer 5

If you're counting cycles in time, frequency is positive. However, the mathematical concept has other, more abstract uses. It is common in Fourier analysis to treat frequency as signed. When using Laplace transforms to analyze linear systems, we use complex frequency.

Answer 6

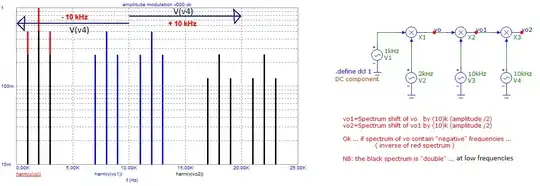
Here is a picture that explains ... what I meant.

The "multiplication of the "vo1" spectrum by a sinusoid (at 10 kHz) give the "vo2" spectrum.
It gives, shifted to the right, the 6 "waves" at 17, 18, 19, 21, 22, 23 kHz.
It gives, shifted to the left, also 6 "waves" at 1, 2, 3 AND -1, -2, -3 kHz (these last 3 are not shown).
These last 3 combine with 1, 2, 3 and give amplitude multiplied by 2.
So, "negative" frequencies are "real" things but only in combination with the real waves at positive frequencies.

What you see in "black" is the recombination (at low frequencies) of the "two" half-spectrums (shifted positive and negative by 10 kHz) which is then "double" amplitude of the six right "waves".

Made with microcap v12.

And here is the Maple sheet ... which details the "amplitudes".

Answer 7

It depends on your definition of frequency.

• "How many times it happens per unit of time"

In this case, it cannot happen a negative number of times, thus frequency is always positive.

• "Instantaneous frequency"

If you have a signal \$ s=sin( \omega t + \theta )\$ you can define its phase as \$ \varphi(t) = \omega t + \theta \$ so your signal becomes \$ s=sin( \varphi(t) )\$.

Now if you use complex notation, or if you have IQ modulation so both the real and imaginary part of the signal are transmitted, it becomes:

\$ s=e ^ { \omega t + \theta } = e^{\varphi(t)}\$

So we have \$ \omega = \frac{d\varphi}{dt} \$ and \$ f = \frac{d\varphi}{\pi dt} \$

Basically, the instantaneous frequency is the derivative of phase \$/\pi\$.

There is no reason the sign of this quantity should be constrained to positive. The real and imaginary components model a rotating vector, if what generates the signal decides to have it rotate in the other direction then \$ \frac{d\varphi}{\pi dt} \$ will change sign.

For example, consider three phase power.

\$ L_1 = A cos( 2\pi f t + 0 ) \$

\$ L_2 = A cos( 2\pi f t + 2\pi/3 ) \$

\$ L_3 = A cos( 2\pi f t + 4\pi/3 ) \$

Just like complex signals, or IQ modulation, that's a vector, it rotates, it can rotate in both directions, and the sign of the frequency is the direction or rotation.

If you don't believe frequency can be negative,

1. Write "rpm = frequency *60 *2 /number of poles" on a post-it.

2. Stick it on a three phase induction motor, for example a pump.

3. Swap two phases and start it.

This only works if the sine signal is a vector (ie, you have at least two actual signals). If the sine signal is a scalar, then positive and negative instantaneous frequencies cannot be distinguished.