The following is from the book Design of Analog CMOS Integrated Circuit, page 207.
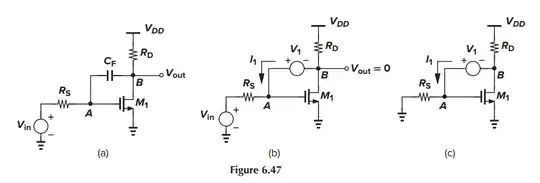
Find the transfer function of the circuit in Fig. 6.47(a):
Suppose the voltage at node A is \$V_x\$.
with the use of KCL at node B,
$$V_x g_{m1} + \frac{V_{out}} {r_o} = (V_x - V_{out}) s C_F - \frac{V_{out}} {R_D}$$
For \$V_x\$, with voltage divider (\$R_S\$ and \$C_F\$).
$$V_x = \frac{V_{in} - V_{out}} {R_S + 1/(s C_F)} \frac{1} {s C_F} + V_{out} $$
$$\Rightarrow \frac{V_{out}} {V_{in}} = \frac{(s C_F - g_m)} {s C_F R_S (g_m + 1/r_o + 1/R_D) + (s C_F + 1/r_o + 1/R_D)}$$
However, the arthor gave this.
$$G(S) = -g_m (R_D \parallel r_o) \frac{1- \frac{1} {g_m} C_F s} {1 + \biggr[(1 + g_m R_D) R_S + R_D \biggr] C_F s}$$
The zero is the same but the pole is different.
roin their derivation of the driving point impedance. The exactZin,0should be[(1 + gm * Rs) * (RD || ro) + Rs]. – internet Jan 16 '24 at 19:17roor not depends on the relative values ofRDandro. As you can see, there is the termRD || ro. IfRDis much smaller thanro, you can ignorero. – internet Jan 16 '24 at 19:23