Why does 'Rfb' affect input impedance?

Question

I am reading "Experimental Methods in RF Design" by Hayward, Campbell, and Larkin published by the ARRL. On the topic of feedback, see that two methods are presented.

One method is emitter degeneration. This makes sense to me; rise in collector current = a rise in emitter current and pushing this through an emitter resistor raises the emitter voltage so Vbe decreases limiting gain and increasing stability.

The other method is collector-base feedback through a resistor 'Rfb'. My intuition tells me that if the collector voltage is at a negative peak, the emitter is at a positive peak. The addition of Rfb pulls the voltage of the base towards negative (sum of base and collector voltages) which brings base voltage closer to Ve, thus decreasing Vbe and causing negative feedback. (Please correct me if that is inaccurate.)

My questions is why the addition of Rfb would affect input impedance. Is it as simple as causing R1 || R2 ||(Rfb+R5) to be seen by a signal going into the input vs just R1||R2? Or is it something closer to the answer on this post: Bootstrapping capacitor effect on impedance

Answer 1

You've already selected an answer and have some good answers. The Miller effect is key to seeing why the input impedance will usually be less than \$R_{_\text{FB}}\$ (diminished by a factor related to the closed loop gain.)

But I was interested in testing my understanding of the well-known linearized hybrid-\$\pi\$ model of the BJT for this problem. (It's been a while.)

^{simulate this circuit – Schematic created using CircuitLab}

The model only works for a tiny range around a known DC operating point. So the DC operating point's quiescent current \$I_{_{\text{C}_q}}\$ must be found, first.

An operating temperature should be selected so that \$V_T\$ can be determined or else just use a rough value between \$25\:\text{mV}\$ and \$28\:\text{mV}\$. I selected \$V_T=25.9\:\text{mV}\$.

Finally, a guess for \$\beta\$ at the operating temperature and \$I_{_{\text{C}_q}}\$ is needed. Usually a typical value can be found in a chart found on the BJT's datasheet. I chose \$\beta=200\$.

All BJTs have a dynamic slope (tangent to their I-V curve) determined by \$I_{_{\text{C}_q}}\$, called \$r_e^{\:'}=\frac{V_T}{I_{_{\text{C}_q}}}\$. I think it is a bit of a misnomer, defined that way, as \$r_e^{\:'}\$ is treated as though it resides at the emitter tip (hence the e in the name) while being defined mathematically by the collector current.

A better term might be to use is its inverse, \$g_m=\frac1{r_e^{\:'}}=\frac{I_{_{\text{C}_q}}}{V_T}\$. Then \$r_\pi=\frac{\beta}{g_m}=\beta\cdot r_e^{\:'}\$. But \$r_e^{\:'}\$ just crops up as a useful idea (as we'll see, shortly.) It sticks around because it is handy.

Although I won't use it, \$r_o\$ is illustrated on this chart below, taken from Ian Getreu's, Modeling the Bipolar Transistor, 1976 (himself citing W. J. McCalla's earlier paper.) It gives an idea about what it is modeling -- the slope to the right of \$V_{_\text{BC}}=0\:\text{V}\$:

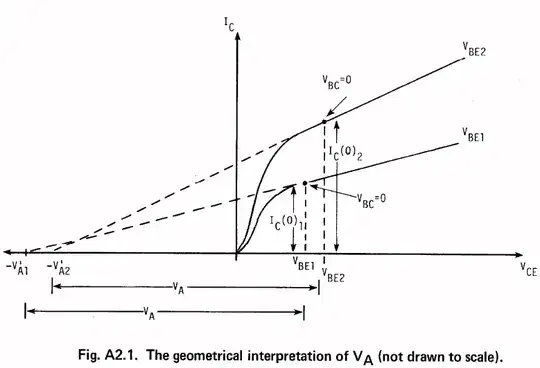
Then \$r_o=\frac{V_A+V_{_\text{CB}}}{I_{_{\text{C}_q}}}\$. (Sometimes this is simplified to \$r_o=\frac{V_A}{I_{_{\text{C}_q}}}\$ or, I believe, also written slightly incorrectly as \$r_o=\frac{V_A+V_{_\text{CE}}}{I_{_{\text{C}_q}}}\$.)

I'm ignoring \$r_o\$ in your case, as \$r_o\$ won't be much of a factor. So, the following analysis doesn't include it.

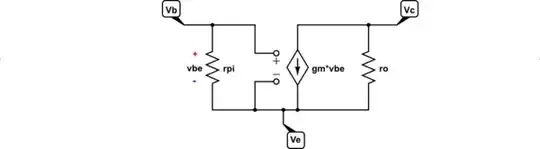
With that, the small signal BJT model can now be inserted into your circuit:

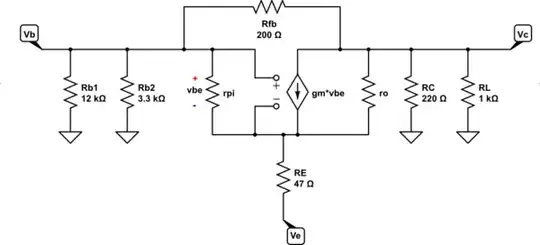
^{simulate this circuit}

Using freely available SymPy and applying KCL to the above I get:

eq1 = Eq( ve/rpi + ve/re, vin/rpi + gm*(vin-ve) )
eq2NoNFB = Eq( vout/rc + vout/rl + gm*(vin-ve), 0 )
simplify(solve( [ eq1, eq2NoNFB ], [ vout, ve ] )[vout]/vin)
-gm*rc*rl*rpi/(gm*rc*re*rpi + gm*re*rl*rpi + rc*re + rc*rpi + re*rl + rl*rpi)

I can define the AC impedance at the emitter, as seen by the collector, as \$r_{ac}=\frac{\beta+1}{\beta}\cdot R_{_\text{E}}+r_e^{\:'}\$. (Just made up the name. But I'm sticking with it here. And here, note, that \$r_e^{\:'}\$ just became useful!)

Then the gain without NFB but including emitter degeneration is \$A_v=-\frac{R_{_\text{C}}\,\mid\mid\, R_{_\text{L}}}{r_{ac}}\$.

The following analysis using SymPy now adds the NFB caused by \$R_{_\text{FB}}\$:

eq2NFB = Eq( vout/rc + vout/rl + gm*(vin-ve) + vout/rfb, vin/rfb )
simplify(solve( [ eq1, eq2NFB ], [ vout, ve ] )[vout]/vin)
rc*rl*(gm*re*rpi - gm*rfb*rpi + re + rpi)/(gm*rc*re*rfb*rpi + gm*rc*re*rl*rpi + gm*re*rfb*rl*rpi + rc*re*rfb + rc*re*rl + rc*rfb*rpi + rc*rl*rpi + re*rfb*rl + rfb*rl*rpi)

Parsing that, in the context of the prior result for \$A_v\$ and the standard NFB equation where \$G=\frac{A_v}{1+\beta_{_\text{NFB}}\,\cdot A_v}\$, I find that the NFB factor can be expressed as \$\beta_{_\text{NFB}}=\frac{\left[\frac{r_{ac}}{R_{_\text{C}}\,\mid\mid\, R_{_\text{L}}}+1\right]}{\left[\frac{R_{_\text{FB}}}{r_{ac}}-1\right]}\$.

In your circuit case, and assuming \$\beta=200\$ and ignoring the Early Effect, I get \$I_{_{\text{C}_q}}\approx 6.2266\:\text{mA}\$ with \$r_e^{\:'}\approx 4.160\:\Omega\$, \$r_\pi\approx 831.9\:\Omega\$ and \$g_m\approx 0.2404\$ for the DC operating point. From these, I estimate \$A_v\approx -4.281\$ (without NFB.) I also estimate that \$\beta_{_\text{NFB}}\approx 0.42664\$. So \$G=\frac{-4.281}{1+0.42664\cdot 4.281}\approx -1.515\$.

The input impedance will be dominated by the feedback resistor. Just divide its value by \$1+\mid\! G\mid\$ and get an estimate of about \$79.5\:\Omega\$. It will be a little lower, of course. Just the \$3.3\:\text{k}\Omega\$ and \$12\:\text{k}\Omega\$ biasing pair alone will drop this to about \$77.1\:\Omega\$. And there will be a little more coming off because of base loading.

I've performed the above calculations without your load resistance included.

To include it, I'll do everything over but this time using the parallel impedance of \$R_{_\text{C}}\$ and \$R_{_\text{L}}\$ (about \$180\:\Omega\$.) Here I get \$A_v\approx -3.50870\$ (without NFB) and \$\beta_{_\text{NFB}}\approx 0.444414\$ and \$G\approx -1.371\$. Input impedance will then be about \$81.692\:\Omega\$. (A little higher than before the circuit was loaded down because now \$G\$ is lower.)

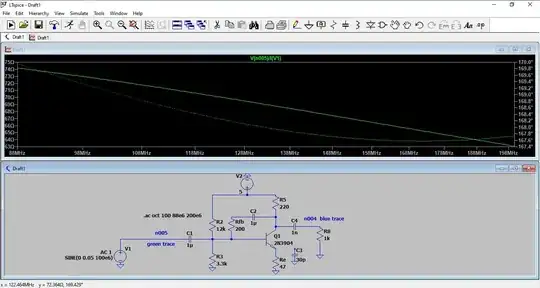
I've not yet run LTspice on these. And I'm frankly a little worried as I'm stretching a simple linearization a bit far. But it's time for verification of the above work product. (I'll set the capacitor values about 100 times higher than you did, just to be sure they don't impact things much.)

First up is the unloaded case:

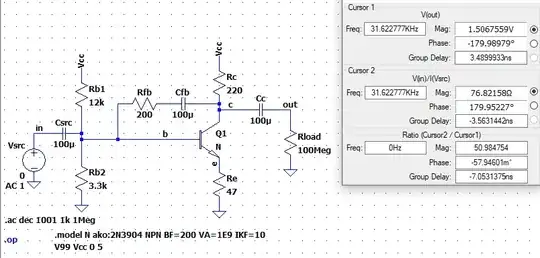
(Note: IKF being set high ensures that I don't get problems with high currents where the \$\beta\$ goes to heck. This will likely mean that the resulting simulation \$\beta\$ will be close to how I set it. And VA being also set very high ensures that we aren't dealing with secondary effects due to the Early Effect.)

Well, here it says \$\mid G\!\mid\approx 1.507\$ vs the above estimate of \$\mid G\!\mid\approx 1.515\$ and that the input impedance is \$\approx 76.82\:\Omega\$ vs the above estimate where I expected it to be slightly less than \$77.1\:\Omega\$.

Next up is the loaded case:

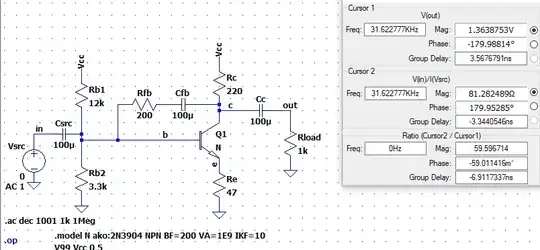
Here it gives \$\mid G\!\mid\approx 1.364\$ vs the above estimate of \$\mid G\!\mid\approx 1.371\$ and that the input impedance is \$\approx 81.3\:\Omega\$ vs the above estimate where I expected it to be slightly less than \$81.7\:\Omega\$.

I'm satisfied.

Answer 2

Resistor \$R_{FB}\$ supplies negative feedback and, if the BJT were replaced with an ideal op-amp, the "base node" would be called a virtual ground and, a virtual ground presents close to zero ohm impedance. It's the same sort of story with a BJT but, the open-loop voltage is not as high.

However, despite the lower voltage gain, it will still make the base node quite a low impedance to ground.

Answer 3

Yousif A, have you ever heard about the Miller effect ?

1. Due to this effect, each part that is located between collector and base appears (as seen from the base) with decreased resistive properties. This is because of the reversed polarity between base and collector: The positive going base potential causes a negative going collector potential - and the current through this path is larger if compared with the case of a fixed collector potential.

2. Therefore, the input resistance in your case contains a value for the Rfb path that is lower than the Rfb value. The reduction factor is app. the gain of thius stage.

3. As another explanation: Voltage-controlled current feedback always reduces the input resistance.

4. As another example, the feedback resistor Rfb in an opamp circuit appears (as seen from the input) with a value Rfb/Aol (open-loop hain Aol). Normally, this value is so small that we can treat it as "zero". This is another explanation for the well-known effect we call "virtual ground".

5. Finally, the input resistance you are looking for is:

   Ri=R1||R2||(Rfb/A)||(hie+hfe*Re)

   Explanation: Transistor gain A=gm(R5||R8)/(1+gmRe) and hie=rbe ; hfe=beta.

Answer 4

My questions is why the addition of Rfb would affect input impedance. Is it as simple as causing R1 || R2 ||(Rfb+R5) to be seen by a signal going into the input vs just R1||R2? Or is it something closer to the answer on this post: Bootstrapping capacitor effect on impedance

The answer "Bootstrapping capacitor effect on impedance" is somewhat different than EMRFD's circuit. Bootstrapping is done to cause bias resistors to affect input resistance less. Not so in EMRFD: bias resistors reduce input Z directly. As other answers mention, Miller effect combined with amplifier gain causes shunt Rfb to affect input Z more than you might expect.

OP's test circuit is complex (pun intended) when it operates at 100 MHz where the 2N3904's model causes the terms "in-phase" and "out-of-phase" to be in-between. Analyzing this situation may make your brain hurt (it does mine).
However, in general terms for an inverting amplifier:

• shunt feedback (Rfb) tends to lower input impedance by the Miller mechanism
• emitter resistor type feedback (Re) tends to raise input impedance.
• shunt feedback (Rfb) couples output to input, making input impedance dependent on output impedance whereas (Re) feedback tends to raise input Z regardless of output.
• Shunt feedback (Rfb) makes input Z gain-dependent
• Both types of feedback tend to decrease gain
• Both types extend the frequency band where gain is flat (constant).
• Both types of feedback tend to improve linearity.
  

---

In an effort to relieve brain stress, use that LTspice model at much lower frequency than 100 MHz: down to 1kHz where transistor phase shifts are far less complex. The 2N3904 biases at 6.6994 mA.
Its inherent R(base-emitter) input resistance is 1221 ohms for AC signals. This is with emitter-to-GND resistor zero ohm rather than 47 ohms.
Bias resistors R2, R3 are in parallel with R(base-emitter), lowering input impedance to 828 ohms.
When you add Re=47 ohms, input impedance looking into the base jumps up to 15052 ohms. Now the bias resistors dominate overall input resistance: 2208 ohms

Now lets add some shunt feedback (Rfb=200):
Input resistance drops to 81 ohms.
You can see that Rfb has now radically dropped input impedance much more than its printed value of 200 ohms, dropping input Z from 2208 ohms down to 81 ohms.

EMRFD favour this combined shunt/series feedback amplifier, because you can combine Re and Rfb in such a way as to maintain input Z near 50 ohms - a common impedance in amplifier signal chains.