How do I apply nodal analysis to this circuit?

Question

Looking at the diagram below, I see the formation of a supernode that is different from the ones I've encountered before and I really don't know how to go about it.

How can nodal analysis be used to solve this circuit?

Answer 1

Take the node 'b' to be the reference. Apply KCL at node 'a'. You will get an equation with two unknowns: 'io' and 'i1'. Also, in the left loop, i1=-io. You now have two equations and two unknowns. Solve this to get the values of the unknowns.

Answer 2

Well, the circuit we want to analyze is given by:

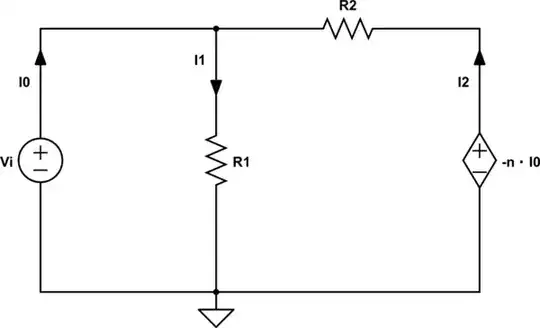
^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \text{I}_1=\text{I}_0+\text{I}_2\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\frac{\displaystyle\text{V}_\text{i}-0}{\displaystyle\text{R}_1}\\ \\ \text{I}_2&=\frac{\displaystyle\left(-\text{n}\cdot\text{I}_0\right)-\text{V}_\text{i}}{\displaystyle\text{R}_2} \end{alignat*} \end{cases}\tag2 $$

Using \$(2)\$ we can rewrite \$(1)\$ as follows:

$$ \frac{\displaystyle\text{V}_\text{i}-0}{\displaystyle\text{R}_1}=\text{I}_0+\frac{\displaystyle\left(-\text{n}\cdot\text{I}_0\right)-\text{V}_\text{i}}{\displaystyle\text{R}_2}\space\Longleftrightarrow\space\text{I}_0=\frac{\displaystyle\frac{\displaystyle\text{V}_\text{i}}{\displaystyle\text{R}_1}+\frac{\displaystyle\text{V}_\text{i}}{\displaystyle\text{R}_2}}{\displaystyle1-\frac{\displaystyle\text{n}}{\displaystyle\text{R}_2}}=\frac{\displaystyle\text{V}_\text{i}\left(\text{R}_2+\text{R}_1\right)}{\displaystyle\text{R}_1\left(\text{R}_2-\text{n}\right)}\tag3 $$