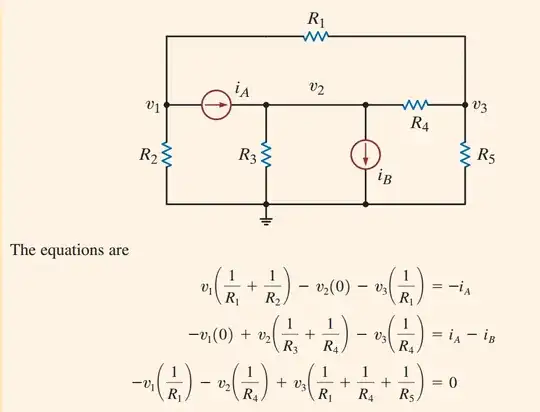
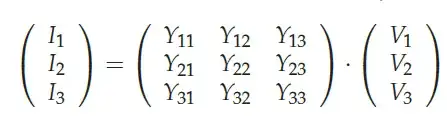0

example problem from circuit analysis book ervin

In this diagram, we see node V2, I can understand how it can be treated as a node. But I don't understand in the equation how \$-v2(0)\$ comes.

I thought maybe the R for short circuit is 0, then also if we take KCL, it becomes \$v2/R = V2/0 = V2*\infty\$. But why is \$-v2(0)\$ in equation no. 1 and also \$v1(0)\$ in equation no. 2?

I want to understand the equations and nodal analysis special cases like this.

JYelton
  • 34,119
  • 33
  • 145
  • 265
Fredrick
  • 119
  • 5
  • 2
    As it stands (with no further information provided), it makes no sense to me to have $v_2(0)$ in the first equation. – Andy aka Dec 12 '23 at 13:21
  • Per Andy's comment, I agree. The dimensions don't even work out. You've got the sum of a current (first term), a voltage (second term), and a current (third term) being set equal to a current. The one item in there that cannot be added is the second term, a voltage. it's just nonsense. What's the source of all this? – periblepsis Dec 12 '23 at 16:29
  • 1
    Fredrick, the equations are:$$\begin{align} \frac{v_1}{R_1}+\frac{v_1}{R_2}+i_{\text{A}}&=\frac{v_3}{R_1} \\ \frac{v_2}{R_3}+\frac{v_2}{R_4}+i{\text{B}}&=\frac{v_3}{R_4}+i{_\text{A}} \\ \frac{v_3}{R_1}+\frac{v_3}{R_4}+\frac{v_3}{R_5}&=\frac{v_1}{R_1}+\frac{v_2}{R_4} \end{align}$$That's it. I'll let you work out how this compares with what you wrote. – periblepsis Dec 14 '23 at 05:58

1 Answers1

0

These equations represent that of a matrix multiplication: enter image description here

I = Y . V

where V is a matrix of nodal voltages, Y is a matrix of admittances connected to/between the node/nodes represented by the matrix element subscripts, I is the remaining current source connected to the nodes corresponding to V.

Now if we think about it, element Y12 is the admittance between nodes 1 and 2, which is zero since the resistance of the current source Ia is infinite.

This gives a product of nodal voltage and Y11 => v2*0. This is just a complicated way of saying KCL at v1 is not influenced by v2. The matrix equations might complicate simple circuits but come in handy while solving bigger networks or while writing lines of code for nodal analysis.

AlveyFrost
  • 65
  • 7
  • Hi I understand the matrix multiplication, but I am quite sure how in the first equation, you see, v2(0) and in second equation v1(0) – Fredrick Dec 12 '23 at 12:23
  • @Fredrick, Y21 = Y12; so the first term of the second equation is also v1y21 = v10. Can you be clear about what you are not sure about? – AlveyFrost Dec 12 '23 at 13:34
  • @Fredrick I think what you need to explain to us is what you think v2(0) and v1(0) happen to be. I certainly have no clue what those are supposed to mean. If you are reading this somewhere, then there is much more context that I think we are missing. And since it also appears you don't know what they mean, I think there must be another source for them and you need to disclose it. – periblepsis Dec 14 '23 at 13:33
  • @periblepsis In case you like a further reference to the matrix multiplication in nodal analysis, you can refer Example 18.1 (Chapter 18) Network Theory of this book: https://open.umn.edu/opentextbooks/textbooks/1497

    The title of the book is Structured Electronics Design: A Conceptual Approach to Amplifier Design - 3rd ed. written by Anton J.M. Montagne, Delft University of Technology

     – AlveyFrost Dec 14 '23 at 15:25
  • @AlveyFrost I wasn't writing to you. Just asking Fredrick for clarification. Note I've written these here, here, here and here, for example. So I feel I'm fine. May not be. That's always at question. ;) – periblepsis Dec 14 '23 at 21:35