0

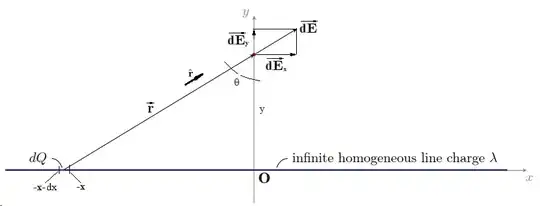
Problem: I am currently tackling a problem involving the derivation of the electric field \$\textbf{E}\$ at location \$(0,y)\$ induced by an infinite homogeneous line charge \$\lambda\$ (refer to the provided image below). I have formulated the integral (last equation below).

Goal: Prior to seeking a solution, my primary aim is to ensure the accuracy of my derivation up to the last equation.

Question: Could you kindly review the equation and point out any errors or suggest improvements? I am solely interested in verifying the correctness of my derivation at this stage and not seeking a solution. Your insights would be greatly appreciated.

enter image description here

First, let's calculate an infinitesimally small charge \$dQ\$ on the line charge:

\begin{align} dQ = \lambda \cdot dx \end{align}

The electric field \$d\textbf{E}\$ generated by this infinitesimally small charge \$dQ\$ is defined as:

\begin{align} d\textbf{E} &= k \cdot \frac{dQ}{\Delta r^2} \cdot \frac{\Delta\textbf{r}}{\Delta r} = k \cdot \lambda \cdot \frac{dx}{\Delta r^2} \cdot \frac{\Delta \textbf{r}}{\Delta r} \end{align}

with the constant by Coloumb's law:

\begin{align} k=\frac{1}{4\cdot \pi \cdot \epsilon_0} \end{align}

and the displacement vector from \$dQ\$ to the point \$(0,y)\$:

\begin{align} \Delta\textbf{r}=\textbf{p}-\textbf{r}= y\cdot \hat{\textbf{y}} - (-x\cdot \hat{\textbf{x}})= y\cdot \hat{\textbf{y}} + x\cdot \hat{\textbf{x}} \end{align}

and the magnitude of the displacement vector:

\begin{align} \Delta r=\left|\Delta\textbf{r}\right|=\sqrt{x^2 + y^2} \end{align}

Proceeding to evaluate the integral:

\begin{align} \textbf{E} &= k \cdot \lambda \cdot \int\limits_{-\infty}^{\infty} \frac{1}{\Delta r^2} \cdot \frac{\Delta\textbf{r}}{\Delta r} \,\, dx \\ &= k \cdot \lambda \cdot \int\limits_{-\infty}^{\infty} \frac{1}{x^2 + y^2} \cdot \frac{x\cdot \hat{\textbf{x}} + y\cdot \hat{\textbf{y}}}{\sqrt{x^2 + y^2}} \,\, dx \\ &=\color{red!60!black}{ k \cdot \lambda \cdot \int\limits_{-\infty}^{\infty} \frac{-x\cdot \hat{\textbf{x}} + y\cdot \hat{\textbf{y}}}{(x^2 + y^2)^{\frac{3}{2}}} \,\, dx} \end{align}

Marco Moldenhauer
  • 121
  • 7
  • 1
    You should explain what lambda and k is. You also explain why you make a distinction between $r$ and $\text{r}$. I know lambda is the line charge density but, I was scratching my head about k. – Andy aka Dec 03 '23 at 10:32
  • @Andyaka: thank you. I edited my question. I hope its clear now. – Marco Moldenhauer Dec 03 '23 at 10:57
  • @Andyaka: How to render inline LaTeX equations here in this forum? BR – Marco Moldenhauer Dec 03 '23 at 11:11
  • The electric field intensity due to an infinite line of positive charge is: |E|=λ/(2πεy) and is directed along y. The potential difference between two points at radial distances r2 and r1 with r2>r1 is: V21=λln(r2/r1)/(2πε) – Franc Dec 03 '23 at 11:22
  • 1
    @MarcoMoldenhauer here's an example $k=\dfrac{1}{4\cdot\pi\cdot\epsilon_0}$ = \$k=\dfrac{1}{4\cdot\pi\cdot\epsilon_0}\$ – Andy aka Dec 03 '23 at 11:33
  • @Franc: thanks a lot but please note that I do not need the final solution. I do need to know if the integral (last equation) is correct or not. – Marco Moldenhauer Dec 03 '23 at 11:34
  • It's an exercise that you can find in all physics and electromagnetics texts. You don't need to ask on this site. – Franc Dec 03 '23 at 19:29
  • @Franc: Ok than it should be easy. is my last equation correct? because i could not find it in any book the way I didi it. – Marco Moldenhauer Dec 04 '23 at 02:21
  • 1
    It seems correct to me. In the integrand, the term in x is symmetric with respect to the y axis so the integral is zero. However, the integral with respect to x of the term in y is not zero. If you had chosen an x on the positive axis, you would have the same result. – Franc Dec 04 '23 at 09:43
  • @Franc: thanks. you can reply to my question then I can upvote and accept your answer – Marco Moldenhauer Dec 04 '23 at 10:33
  • 1
    I would highlight on the graph the vector E aligned with the unit vector r and its two orthogonal components. I would also define r as the position vector. The formulas are correct. – Franc Dec 04 '23 at 11:21
  • @Franc: I have implemented the modifications you suggested. I hope the content has improved. Best regards. – Marco Moldenhauer Dec 05 '23 at 06:52
  • @Franc: Can you please check the displacement $\Delta\textbf{r}$ vector equation. – Marco Moldenhauer Dec 05 '23 at 07:02

1 Answers1

0

I was referring to the previous graph, the current one is not acceptable. enter image description here

Franc
  • 1,126
  • 1
  • 9