1

I have just recently started studying electric circuits, and as far as I know if a cell has a potential difference of V, we can assume the negative terminal of the battery to have 0V potential and positive terminal to have V volts potential. I have solved a number of problems in this manner, and always got the correct answer, however I am having doubts when solving circuit problems involving more than 1 Cell.

So, my question is, when a circuit has two cells of emf V1 and V2, can we assume that the negative terminals of both the cells have 0 potential and the positive terminals have V1 and V2 potentials respectively? If not, then why?

As an example, see the problem number 25 part (b). Why can't I take the negative terminals of both cells in this problem as 0V and the +ve terminals as 12V and 24V respectively and then say the potential difference between a and b is 0V? The answer to the problem is -8V

enter image description here

Marcus Müller
  • 94,373
  • 5
  • 139
  • 252
Aditya Mukherjee
  • 21
  • 4
  • Imagine your (b) circuit is floating the great voids of outer space between super-clusters of galaxies. It's totally alone. What's the voltage at any node in the circuit? (It still works just fine.) It should be impossible to say. All that you can say about any of it is that the nodes have *relative* voltages to each other, but that the values themselves at the nodes are arbitrary. You can add one million to all of them and nothing changes. Or subtract that much and nothing changes. Still works, too. The absolute numbers are meaningless. So you get to pick any one of them and call it zero. – periblepsis Oct 22 '23 at 12:46
  • @periblepsis , ok, so it is just a convenient assumption, so that we can solve the problem, right? – Aditya Mukherjee Oct 22 '23 at 12:49
  • You can solve the problem by assuming one of the nodes is one, too. Or, if you like it abstract, then x and just leave it to be filled out later when you feel like it. (Keep in mind that a positive end of a voltage source can be assigned 0, or 1, or x, just as easily as any other.) On a more technical note, there's something called the Rank-Nullity Theorem that, applied in graph theory, informs the whole question, rigorously and clearly. But then I'd have to write a lot more. (See here for a sample.) – periblepsis Oct 22 '23 at 13:17
  • @periblepsis , can the reference point for measuring potentials be taken at infinity? – Aditya Mukherjee Oct 22 '23 at 13:21
  • Do you mean in the way that those in orbital mechanics and discussing orbital energy do? – periblepsis Oct 22 '23 at 13:24
  • @periblepsis , no like we do in measuring potential for say like a charged sphere in electrostatics – Aditya Mukherjee Oct 22 '23 at 13:25
  • Okay. Then yes, similar idea. But no, I haven't seen it done. And thinking about it I'm not sure how you would define things to make that work right. Conservation laws and symmetries don't seem to apply. I wouldn't want to stop you from trying, though. – periblepsis Oct 22 '23 at 13:28
  • @periblepsis , yeah it is kind of useless, I can't make it work either – Aditya Mukherjee Oct 22 '23 at 13:33
  • @periblepsis, I have another doubt, it is kind of off topic of this question, but I wanted to ask that can we always say that potential decreases when we move from +ve plate to -ve plate of a capacitor? I think it is true, because the electric field is from the +ve plate to -ve plate. – Aditya Mukherjee Oct 22 '23 at 13:35
  • Let us continue this discussion in chat. – Aditya Mukherjee Oct 22 '23 at 13:35

5 Answers5

2

We don't assume the -ve terminal of a cell to be 0 V.

For many purposes, we define 0 V at the -ve terminal of a cell, because that's the easiest place to put it.

Absolute potentials are undefined. It's convenient to define some particular place to be 0 V. Many simulator programs require some place to be defined as 0 V. We usually choose 0 V to be the metal case, or the conductive ground, the chassis of a vehicle, or whatever's appropriate for where we are working.

If we have two cells connected in a circuit, then it's usually impossible to define both their -ve terminals as 0 V. Consider a 3 V battery made from two AA cells. The 'upper' cell has potentials 1.5 V higher than the lower cell.

Neil_UK
  • 166,079
  • 3
  • 185
  • 408
2

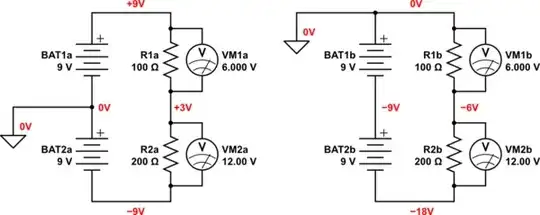
The "voltage" of a cell or battery is only a measure of the potential difference between its two terminals. That is, a 9V battery's positive terminal is known to be 9V more positive (9V higher in potential) than its negative terminal. Those 9V tell you nothing about the the absolute potential of either terminal.

Absolute potential doesn't exist, since there's no point in the universe that you could call "zero" volts, but nothing's stopping you from declaring an artificial "zero" (ground) at any point in your circuit, and quote all potentials elsewhere relative to that. This practice simplifies circuit analysis and descriptions. If you've declared that a 9V battery's negative terminal is "ground" (0V), then it's easier to say that "the positive terminal is +9V", than "the difference in potential between the positive and negative terminals is 9V, and the positive terminal potential is the higher of the two".

This means you could declare either terminal of the battery to be 0V (ground), and since this you do this only as a matter of arithmetic/descriptive convenience, it doesn't change potential differences anywhere, and therefore doesn't change the behaviour of the circuit at all:

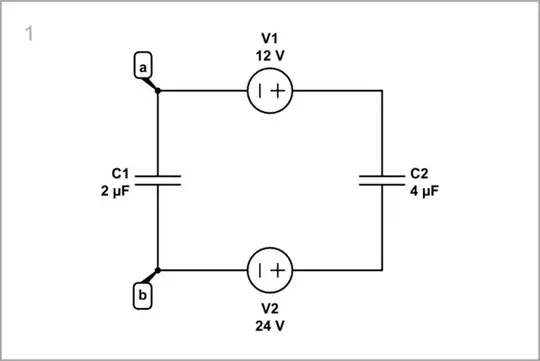
schematic

simulate this circuit – Schematic created using CircuitLab

I've declared "ground", the zero-volt node, in different places in those two circuits, but the voltages across all elements remains the same, the current through all elements remains the same. Behaviour is the same in both cases.

For the purpose of analysis and communication with other engineers, I've marked the "absolute" potentials in red. They aren't really absolute, they're just quoted relative to to our designated zero point.

It also helps that the ground symbol can be used in many places around a schematic, indicating that all such nodes are physically joined, electrically connected together. Considering that this ground point will probably be used by many, many other parts of larger systems, this convention helps keep the schematic uncluttered.

Apart from that, the node we declare to be ground, having a potential of 0V, is completely arbitrary, and doesn't influence circuit behaviour.

Kirchhoff's Voltage Law (KVL) doesn't have a concept of absolute potential, it deals exclusively with potential differences across elements in a loop. This means it's safe to raise or lower all absolute potentials in a circuit by the same amount, without upsetting any KVL results. All KVL says is that whatever absolute potential you start with, at some node in a loop, all the potential increases and decreases that you encounter as you travel around that loop must bring you back to that same potential when you eventually get back to the starting node. In other words, potential change around the entire loop must always be zero, regardless of the absolute potentials at any individual node along that path.

By the way, it seems to me that circuits (b), (c) and (d) in your pictured question don't have a single solution. In those circuits, there are infinitely many solutions to \$V_a - V_b\$. The capacitors can each have any potential difference, as long as KVL isn't violated, and where they settle will depend on their initial charge, battery internal resistance, and the order in which the circuit is assembled.

Simon Fitch
  • 34,939
  • 2
  • 17
  • 105
1

Once you label a circuit node as \$\boxed{\text{0 volts}}\$ you are defining the measurement reference point for any other voltage observations you might make. If you then define another node as \$\boxed{\text{0 volts}}\$ then you are saying "these two nodes are shorted together".

can we assume that the negative terminals of both the cells have 0 potential

Only if they are electrically / galvanically connected.

Andy aka
  • 456,226
  • 28
  • 367
  • 807
0

Original circuit

This circuit (25b) is a loop where KVL is valid. All voltages, including between points a and b, are "floating" (the circuit can not be simulated since CircuitLab needs a ground).

schematic

simulate this circuit – Schematic created using CircuitLab

Transformed circuit

Group the sources into an equivalent voltage source and the capacitors into a capacitive DC voltage divider. Put a ground because the simulator requires it. Then replace the DC constant voltage source with a step voltage source to explore the circuit's operation over time.

schematic

simulate this circuit

Allow for the fact that the current in the circuit is the same, hence the charges of the capacitors are equal, and you will easily find the voltages across them. As you can see, Vab = 8 V.

STEP 2.1

STEP 2.2

Circuit fantasist
  • 16,664
  • 1
  • 19
  • 61
0

It's not an assumption as much as it is a choice. You can also choose to define the positive terminal as 0V. Usually this choice is connected to whether circuits work better with a positive or negative reference ground. With the prevalence of NPN silicon transistors, negative ground became pretty common for most signal processing (well, until opamps mostly called for symmetric power supplies).

For cars, usually the negative pole is connected to the car chassis and defined as 0V. A few old cars have the positive pole connected to the car chassis and consequently as the 0V point. One needs to be rather careful with startup help with those cars (possibly they don't use 12V either).

user107063
  • 3,703
  • 1
  • 3
  • 16