"There's only one way to rock", as old Sammy says and here it's called the fast analytical circuits techniques or FACTs. You can try to use Thévenin to extract the transfer function and it will surely work provided you have a math solver. But if you do it by hand, you may quickly reach algebraic paralysis and even a good glass of wine won't help.
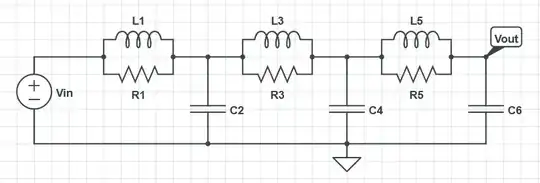
A quick introduction to the FACTs was given in my APEC 2016 seminar that you can look at. It details how poles and zeroes can very often be determined painlessly, without writing a single line of algebra. Look at your circuit below:
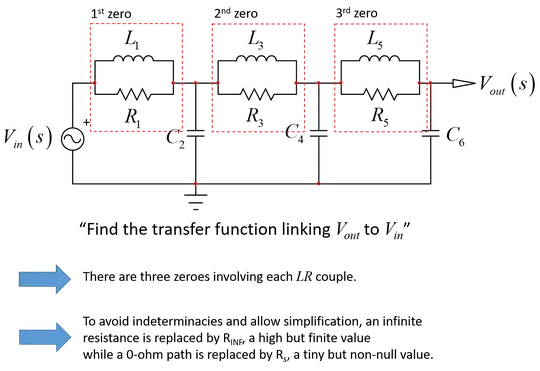
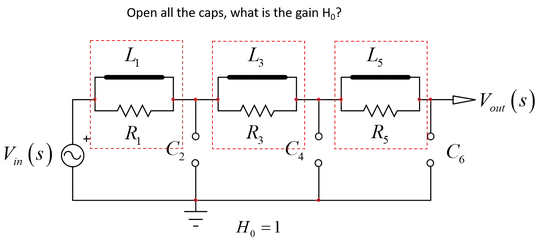
Just by looking at it - and it's not the prestige : ) - I can see 3 zeroes and a unity dc gain:
The zeroes are determined by finding in this circuit one or several particular impedances which can become either an infinite impedance in the path of the stimulus or a transformed shunt, bringing one branch to the ground. Both of these behaviors null the response. It means that despite a stimulus present at the input, it is lost somewhere in the circuit and the output is 0 V ac. By inspecting the circuit, I can already write the numerator:
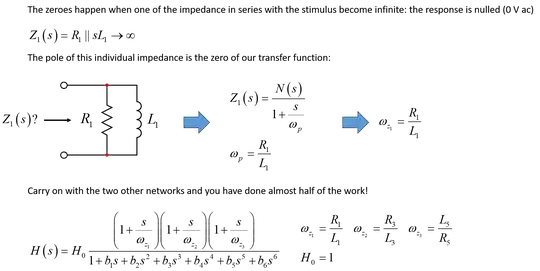
Should you add a small resistance \$r_C\$ in series with \$C_2\$ for instance, you would introduce a 4th zero.
The principle is now to determine the time constants of the circuit when each energy-storing element is set in its dc or high-frequency state (read the seminar) and the stimulus is reduced to 0 V (\$V_{in}\$ is replaced by a short circuit). You will obtain the natural time constants of this circuit which depends solely on the structure of the circuit, without its excitation. Here, we have 6 energy-storing elements with independent state variables so the denominator is of degree 6. I will show you how to determine \$b_1\$ but I'll leave the rest to you:
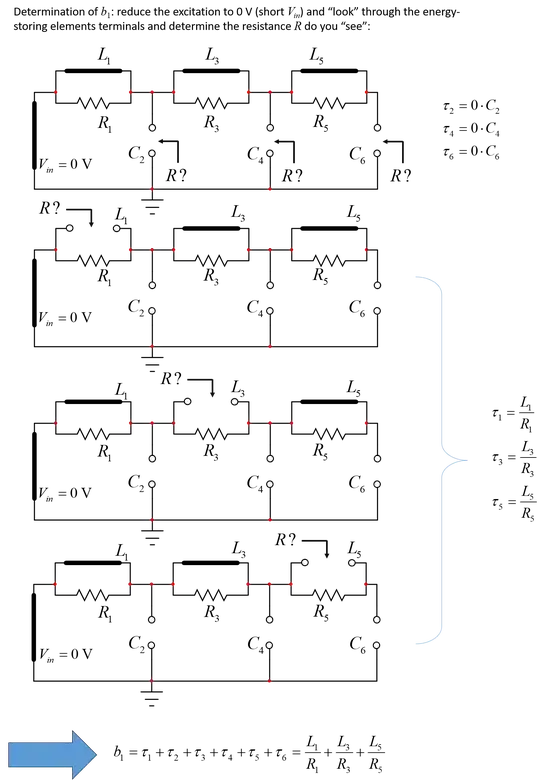
Then you can proceed with \$b_2\$ and follow the explanations I gave in this solved 6th-order example from my web page here. And if you want to adopt the FACTs - highly recommended - then you can have a look at my book on the subject.
If you go step by step or petit à petit in French and carefully craft your drawings, you will make it. The cool thing is that if you find a mistake in the end, no need to restart from scratch, just fix the guilty sketch and see all curves superimposing as in my example, just by magic! Good luck with this example.