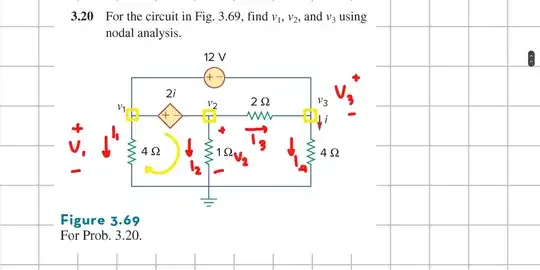
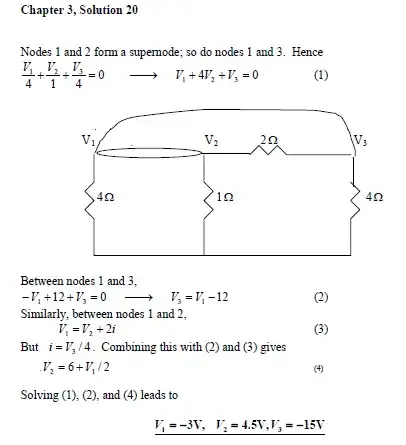
The thing that confuses me is why I3 (in my drawing) is not included
in Equation 1 of the solution, whereas they included I2.
They included exactly and only \$I_1\$, \$I_2\$, and \$I_4\$ (your terms in your drawing) because that's all that should be included.
Just think for a moment. You've got those three currents sinking through those three bottom resistors. It doesn't matter what's going on above them because, in the end, all that stuff going on up there doesn't matter to the currents in those three resistors. They themselves still must sum to zero, regardless. If your \$I_3\$ changes, all that can actually change will be the currents in one or both of those voltage sources.
To prove it to yourself, just analyze the circuit without the use of supernodes.
Label two new currents, pointed leftwards. One current, \$I_{V_D}\$, will be the current in the dependent source. Another current, \$I_{\text{V12}}\$, will be the current in the independent source above the dependent source.
Label your resistors as \$R_1\$, \$R_2\$, and \$R_3\$ for the grounded resistors, working from left to right. The remaining resistor is \$R_4\$.
The KCL is then:
$$\begin{align*}
\boxed{\frac{v_1}{R_1}}&=I_{V_D}+I_\text{V12}
\\\\
\boxed{\frac{v_2}{R_2}}+\frac{v_2}{R_4}+I_{V_D}&=\frac{v_3}{R_4}
\\\\
\boxed{\frac{v_3}{R_3}}+\frac{v_3}{R_4}+I_\text{V12}&=\frac{v_2}{R_4}
\end{align*}$$
Simple as that. Note that I've boxed those three currents (those you've labeled as \$I_1\$, \$I_2\$, and \$I_4\$.) There's a reason for doing that.
Allow me to re-arrange things slightly:
$$\begin{align*}
\boxed{\frac{v_1}{R_1}}&=I_{V_D}+I_\text{V12}
\\\\
\boxed{\frac{v_2}{R_2}}&=\frac{v_3}{R_4}-\frac{v_2}{R_4}-I_{V_D}
\\\\
\boxed{\frac{v_3}{R_3}}&=\frac{v_2}{R_4}-\frac{v_3}{R_4}-I_\text{V12}
\end{align*}$$
Now, what would happen if we added up these three equations? (Left sides together and placed on the left and right sides together and placed on the right.) Do you see your \$I_3\$ anywhere?