Can anyone help me to solve this circuit using node voltage method? Because in the solution, I don't understand why there is just 3I1 only.
1 Answers
Look, I think I completely agree with your process. But before I go there, let's take a look at the schematic again:
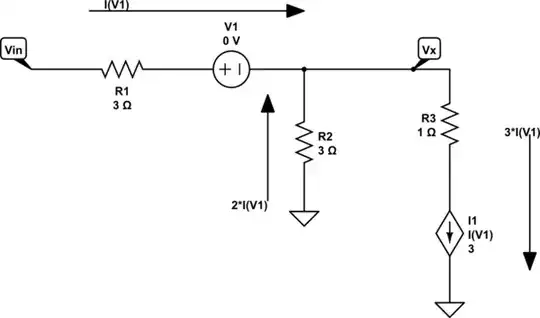
simulate this circuit – Schematic created using CircuitLab
I think you can see why I've set up the currents this way. In order for the currents at \$V_x\$ to sum to zero, the above must be true. The value of \$R_3\$ really doesn't matter much. All it does is change the voltage across \$I_1\$. But otherwise it has no impact on that branch.
Getting back to the KCL (nodal):
$$\begin{align*} \frac{V_x}{R_1}+\frac{V_x}{R_2}+3\cdot I_1&= \frac{V_{_\text{IN}}}{R_1} \\\\ \frac{V_x-V_{_\text{IN}}}{R_1}+\frac{V_x}{R_2}+3\cdot I_1&= 0\:\text{A} \end{align*}$$
And that's pretty much what you wrote, already. So I don't find any problems with your work product.
Since \$I_1=\frac{V_{_\text{IN}}-V_x}{R_1}\$:
$$\begin{align*} \frac{V_x-V_{_\text{IN}}}{R_1}+\frac{V_x}{R_2}+3\cdot \frac{V_{_\text{IN}}-V_x}{R_1}&= 0\:\text{A} \\\\ \frac{V_x}{R_1}+\frac{V_x}{R_2}+3\cdot \frac{V_{_\text{IN}}}{R_1}&= \frac{V_{_\text{IN}}}{R_1}+3\cdot \frac{V_x}{R_1} \\\\ V_{_\text{IN}}&=\left(1-\frac12\frac{R_1}{R_2}\right)V_x \end{align*}$$
From that, and given your resistor values, it's clear that \$V_x=2\cdot V_{_\text{IN}}\$.
So what's your difficulty here? I think you did just fine.
- 8,575
- 1
- 4
- 18
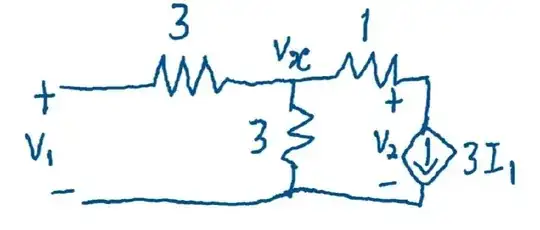

node method. So I'm not quite understanding what you feel you need to hear. Or is that a copy of notes you took, but don't follow? – periblepsis Jul 01 '23 at 00:02