Expanding BW using feedback

Question

I have built the following two stage amplifier as shown below. In open loop I get 63 dB gain and BW about 3 kHz. When I tried to add a feedback resistor to lower the gain and increase the bandwidth as shown in the formula below I get no change at all. Two stage amplifier with feedback is shown in the end.

Where did I go wrong in implementing the feedback effect of feedback resistor to lower the gain and increase the bandwidth?

Answer 1

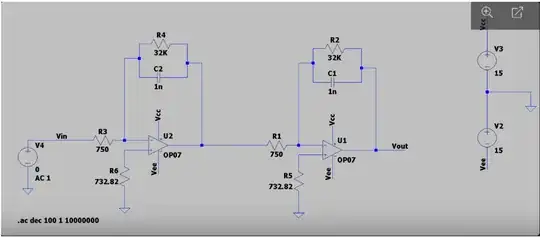
Look at just one stage:

^{simulate this circuit – Schematic created using CircuitLab}

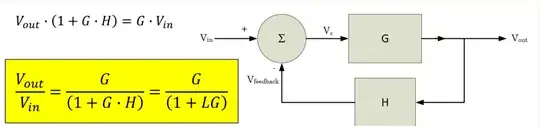
\$V_{_\text{IN}}\$ sees a divider formed between itself and \$V_{_\text{OUT}}\$. That is what gets summed into the wire there at the (-) input. \$V_{_\text{OUT}}\$ sees a divider formed between itself and \$V_{_\text{IN}}\$. That is also what gets summed into the wire at the (-) input. This is then compared with ground, as expected, and the difference multiplied by the open loop gain of the opamp, \$A\$, to get the final \$V_{_\text{OUT}}\$ result.

Using the second stage with lower-numbered parts, start with \$Z_{_\text{IN}}=R_1\$ and \$Z_{_\text{F}}=R_2\mid\mid Z_{_{\text{C}_1}}\$:

def par(a,b): return a*b/(a+b)
Zin = r1
Zf = par(r2,1/s/c1)
n1,d1 = fraction(solve(Eq((0-(vin*Zf/(Zf+Zin)+vout*Zin/(Zf+Zin)))*A,vout),vout)[0])
simplify(n1/A) / expand(simplify(d1/A))
-r2*vin/(c1*r1*r2*s + r1 + c1*r1*r2*s/A + r1/A + r2/A)

And as \$A\to\infty\$ then find \$V_{_\text{OUT}}=-V_{_\text{IN}}\cdot\frac{R_2}{R_1}\cdot\frac{1}{1+R_2\,C_1\,s}\$.

If instead we solve the KCL (\$V_1\$ being the (-) input node) then:

solve(Eq(v1/r1+v1/r2+v1*s*c1,vin/r1+vout/r2+vout*s*c1),vout)[0].subs(v1,0)
-r2*vin/(r1*(c1*r2*s + 1))

Which is the exact same result. So nothing new. But it does show that the feedback diagram above matches your schematic for one stage.

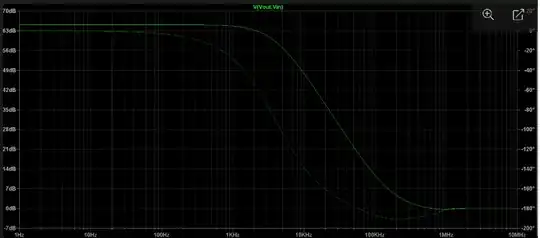
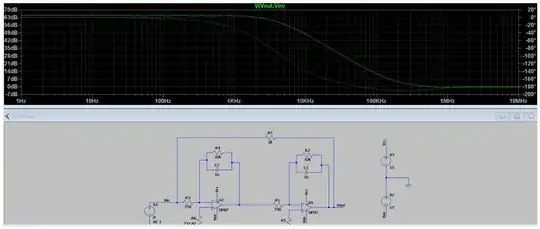
If you are to bring back negative feedback to the pair of stages, note first that your final output is in-phase with the input. (And with both stages, I'd expect about \$65\:\text{dB}\$ gain at the output, discounting opamp details.)

Suppose you wanted to reduce the gain to \$40\:\text{dB}\$ and only make the simplest change (and ignore whatever it does to the \$Q\$ of the circuit.) Then:

def gain(a): return 10**(a/20).n()
solve(Eq(732.82/(732.82+x),solve(Eq(gain(65)/(1+gain(65)*x),gain(40)),x)[0]),x)[0]
76915.6758028831

So, this suggests a feedback resistor of about \$76.9\:\text{k}\Omega\$ connected back to the first stage's (+) input. (Leave the existing grounded resistor in place.) This approach was already suggested in comments. Why don't you try this and see?