Apologies for the not so clear title, but I don't know if there is a common phrase that describes the point of concern.
I am taking an online course about input filter design interfacing the grid and a rectifier. the LC filter as is would not suffice because it has a "resonance" frequency at which the impedance is infinite. this point will ruin the entire system performance of the power electronics rectifier and the regulated voltage at the load.
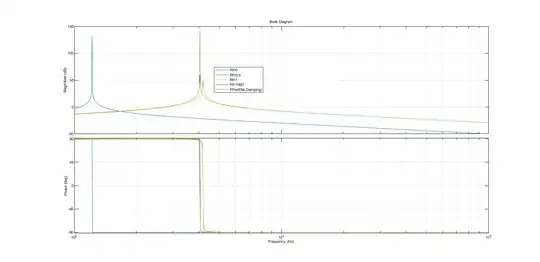
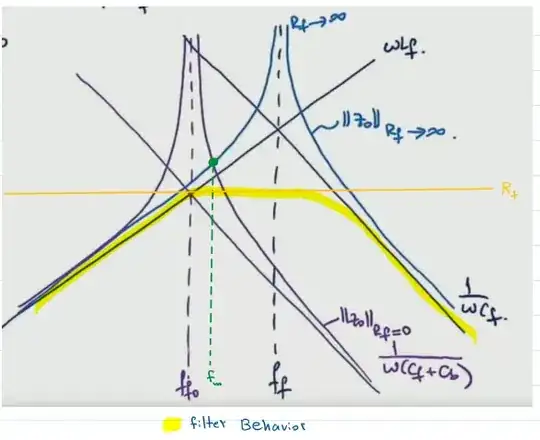
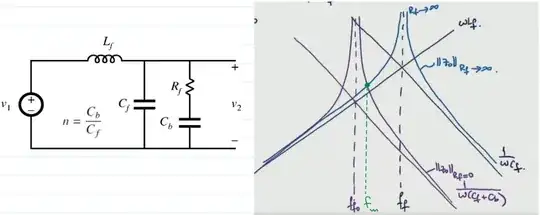
In damping the LC filter, we opted for a series RC in parallel with the LC filter as seen in the figure. Which brings us to my problem, the instructor mentioned that there exist a frequency f_m at which the impedance remains constant, no matter what the value of the added R_f. As you can see in the Bode plot, R_f=0 and R_f=infinity are plotted and there is a point that appears in both cases which is marked at frequency f_m. The instructor quickly mentions that this point will be there no matter what the value of R_f is.
I tried to draw the bode plot by inspection for different R_f values
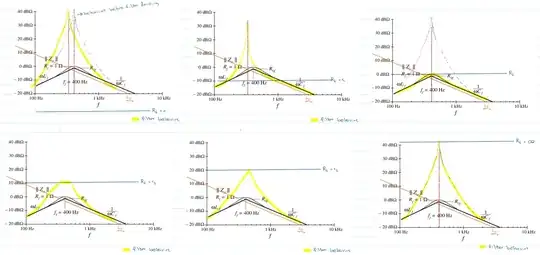
but It appears to me that there is no such frequency f_m which is unaffected by R_f
-----------------Edit----------------
I plotted the transfer function in matlab, and there is indeed a point(f_m) where changing R_f doesn't influence the impedance.