How to find natural frequency from graph/plot of MATLAB Simulink?

Question

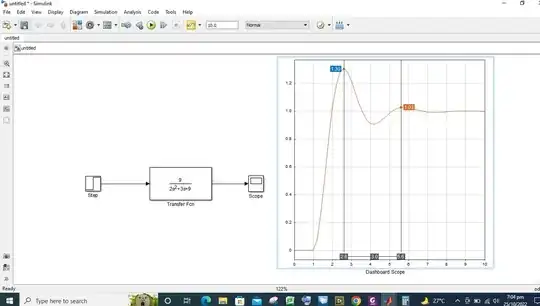
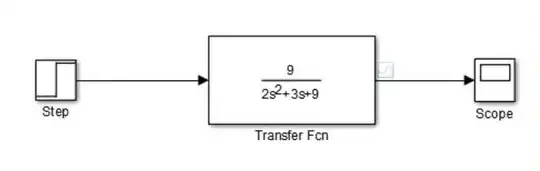
I have compared my transfer function with standard characteristic equation of a 2nd order system and I found out that my natural frequency is 3 radians and damping ratio (zeta) is 0.5 but how can I estimate/find and verify these values from graph/plot of MATLAB Simulink Scope?

I have also attached a snapshot, which shows two data cursors at two consecutive peaks. From those cursors, I found out approximate time period which is approximately 3 second and then from reciprocal of that time period i found out frequency, which is 0.33 Hz and then I multiply it 2 and pi but I get answer as 2.07 radians.

But my transfer function has originally natural frequency of 3 radians, why this difference?

Answer 1

Here's your transfer function: -

And, when you divide through by two in the denominator and numerator you get: -

$$H(s) = \dfrac{4.5}{s^2 +1.5s +4.5}$$

And, that's a natural frequency (\$\omega_n\$) of \$\sqrt{4.5}\$ = 2.12132 radians per second (and not 3 radians per second).

Given that 1.5 = \$2\zeta\omega_n\$ you can figure that out by yourself but, I get 0.3536 and, that would put the damped oscillation frequency at 1.9843 radians per second. (\$\omega_d = \omega_n\sqrt{1-\zeta^2}\$)

Anyway, the bottom line is that your measured value (by computing the time between peaks) is slightly lower than the natural value and this figures right to me.

Answer 2

The natural frequency of your transfer function is not 3, and also the natural frequency of a second order system is not the frequency of the oscillations. the frequency of the oscillations is given by the imaginary part of the poles of your system. The poles of your system are s1 = -0.75 + 1.98i, s2 = -0.75 - 1.98i - so the frequency of the oscillations is expected to be 1.98 rad/s. Running your system in MatLab I got the time period 2.04 s - very close to 1.98.