How to find resistors from E series for a certain ratio?

Question

Given is a ratio for resistors, e.g. two resistors \$\frac{R_1}{R_2}\$ = "some odd value", like 257:42.

How do I find matching resistor pairs (triples, ...) from E series, without having to try them out one by one?

When I search for the title, I merely find tools, which calculate R₂ if the ratio as well as R₁ are given.

However, I want a way which gives me matching resistor values given only the ratio. I did not find any list/table with all ratios or a calculator tool online.

Finding the magnitude is answered here. Another answer talks about "Sallen Key", which seems to be more complicated than my task.

What am I trying to achieve?
I need a certain gain in my measuring chain. When designing the op-amp circuit, I calculated a certain ratio which is needed for the resistors. Only some standard E series ones are available at the moment.

There are online calculators for the very purpose. I used to have a shareware (yes, shareware) desktop application for the very purpose. Very useful. Gladly paid the 5 bucks for it. — winny, Sep 05 '22 at 21:11
What tolerance resistors are you considering using? Will you be happy with the nominal value ratio being correct (rather than measuring and calibrating the resistors)? — Transistor, Sep 05 '22 at 21:12
@winny: Could you maybe share a name of such a tool?
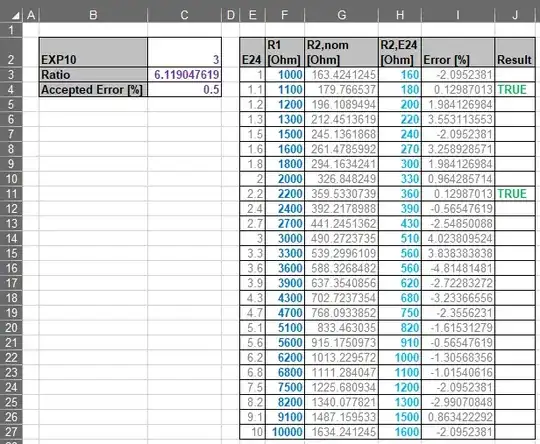
Transistor:I do not know. My plan was to use the nominal value and test if the op-amp setup meets requirements. — Paul Smith, Sep 05 '22 at 21:19
Use 11k and 1.8k, it's accurate to within 0.13% :-) I wrote a small Perl script to do such calculations about 20 years ago; I use it all the time. But there are online calculators, as mentioned above. — Dave Tweed, Sep 05 '22 at 22:00
@PaulfromC You want to first find a resistor series that will accommodate it. To do that, compute $\log_{10}\left(\frac{257}{42}\right)\cdot E_{\text{series}}$, adjusting the selected $E{_\text{series}}$ until you get a near-integer at the output. In this case, it suggests E192, which gives about 151.0433. Close enough. So if you just want a series that will get you there without complex sum-combos, that's one way. From E192 you might select 612 and 100, for example. For sum combos of lesser E series, see rule-notes at end here. — jonk, Sep 05 '22 at 23:59
Thanks for the tool recommendation, It worked well. What I actually looked for was the spreadsheet shared by Seir. — Paul Smith, Sep 06 '22 at 20:58
I wrote a book for that very purpose (back in the early days of the internet) https://books.google.be/books/about/Electronics_Calculations_Data_Handbook.html — danmcb, Sep 14 '23 at 06:20

score 5 · Accepted Answer · answered Sep 06 '22 at 12:01

You can create such a table yourself using Excel and a macro function.

I've created one for the E24 series.

Formulas:

F3 cell: =E3*POWER(10;$C$2)
G3 cell: =F3/$C$3
H3 cell: =GetNearestE24Resistor(G3)
I3 cell: =100*(H3/G3-1)
J3 cell: =IF(ABS(I3)<=$C$4;"TRUE";"")

Drag these formulas to populate all rows.

Macro function:

Function GetNearestE24Resistor(Rnom As Double)
    Dim Reff As Double
    Dim Re24(25) As Double
Re24(0) = 1
Re24(1) = 1.1
Re24(2) = 1.2
Re24(3) = 1.3
Re24(4) = 1.5
Re24(5) = 1.6
Re24(6) = 1.8
Re24(7) = 2
Re24(8) = 2.2
Re24(9) = 2.4
Re24(10) = 2.7
Re24(11) = 3
Re24(12) = 3.3
Re24(13) = 3.6
Re24(14) = 3.9
Re24(15) = 4.3
Re24(16) = 4.7
Re24(17) = 5.1
Re24(18) = 5.6
Re24(19) = 6.2
Re24(20) = 6.8
Re24(21) = 7.5
Re24(22) = 8.2
Re24(23) = 9.1
Re24(24) = 10

Dim F As Double  ' Factor

Dim Rl As Double ' Lower Limit
Dim Ru As Double ' Upper Limit

F = 1

' Find range of the resistor Rnom within the E24 series
Do
    If Rnom &lt; Rl Then
        F = F / 10
    ElseIf Rnom &gt; Ru Then
        F = F * 10
    End If

    Rl = Re24(0) * F
    Ru = Re24(24) * F
Loop Until Rnom &gt;= Rl And Rnom &lt;= Ru

' Find the two nearest E24 resistors
Dim i
For i = 0 To 23
    Rl = Re24(i) * F
    Ru = Re24(i + 1) * F

    If Rnom &gt;= Rl And Rnom &lt;= Ru Then
        Exit For
    End If
Next i

' Find the nearest E24 resisitor
Dim Dl As Double
Dim Du As Double

Dl = Rnom - Rl
Du = Ru - Rnom

If Dl &lt; Du Then
    GetNearestE24Resistor = Rl
Else
    GetNearestE24Resistor = Ru
End If

Exit Function

End Function

StickySli · Answer 2 · 2023-09-14T10:37:19.283

No Visual Basic, just equations. Here's my solution (scroll right for example):

TABLE 1 (CALCULATOR, horizontal)

Named cell	Equation in code style, other in italics	Value (Example)
Input	Data Input	332.5
Multiplier	`=10^INT(LOG10(Input))`	100
Scaled Input	`=Input/Multiplier`	3.325
Target	Dropdown cell with values: 24, 48, 96, and 192	24
Index Exact	`=Target*LOG10(Scaled_Input)`	12.52
Index Rounded	`=ROUND(Index_Exact;0)`	13
Output	`=ROUND(POWER(10^Index_Rounded;1/Target);IF(Target=24;1;2))`	3.5
Output Corrected	`=IF(Target<>24;Output;XLOOKUP(0;ABS(E24_Series#-Scaled_Input);E24_Series#;;1))`	3.30
Output Scaled	`=Multiplier*Output_Corrected`	330

TABLE 2 (E24 series, vertical)

Named cell	Equation in code style
E24_Series	`={1;1.1;1.2;1.3;1.5;1.6;1.8;2;2.2;2.4;2.7;3;3.3;3.6;3.9;4.3;4.7;5.1;5.6;6.2;6.8;7.5;8.2;9.1}`

This is a spilled equation that will expand downwards from a single cell. We use the notation E24_Series# to reference to this dynamic array.

If you prefer not to use this 2nd table, replace E24_Series# with {1;1.1;1.2;1.3;1.5;1.6;1.8;2;2.2;2.4;2.7;3;3.3;3.3;3.6;3.9;4.3;4.7;5.1;5.6;6.2;6.8;7.5;8.2;9.1} in the equations above.

Formatting Note

I have used ; (semicolon) for the argument separator, not , (commas).
I have also used named cells for this make-shift markup Table so it's easier to understand. In Excel, you can name a cell by clicking on it and changing its name to the left of the equation. They can also be checked in the Name Manager under Formulas.

Step-by-step explanation:

We know that the resistor standard series is in a logarithmic scale given the equation \$V_n=\text{round}(\sqrt[m]{10^n})\$, where \$V_n\$ is the rounded value, \$m\$ is an integer of the E series group size, and \$n\$ is an integer of \$\{0,1,2,...,m-1\}\$. Wikipedia - E_series of prefered standard numbers. Therefore, the resulting scaling steps will be between the values of 1 and 10 for this equation in equally-spaced logarithmic steps.
Before doing any calculations, we will need to normalize our input to values between 1 and 10. This is done by finding the logarithm base-10 of the input and taking its minimum (floor, or int, doesn't really matter in this case) so we can get the power of 10 that our input needs to be divided by. This is almost similar to finding the minimum number of bits to encode a number: \$bits=\text{ceil}(\text{log2}(n))\$.
We will now solve the equation of the standard series. This cell is the Index Exact.
Next, the rounding of the index, or finding the closest value to the E-series. Observe that the index is in a linear scale from \$0\$ to \$m-1\$ thus, to find the closest value we just need to round to decimals. This is the Index Rounded.
We found the index \$m\$ of our first equation. We can now solve it, but how many decimals does the rounding require? From experience, I can tell you that for E24 we round to \$1\$ decimal place, and for E48 and above we round to \$2\$ decimal places. This is easier to do with our normalized values.
The Wikipedia article also tells us that for historical reasons, some of the values of E24 are tweaked. This can be corrected in our output equation by using the XLOOKUP with the match mode 1 to find the next closest value (like rounding). I have used a reference to a spilled array for the E24 series, although it can be replaced with a constant array.Observe how the \$332.5\$ value in the example is detected as index \$13\$ which is the multiplier \$3.6\$, but afterwards it is corrected by finding the best suitable resistor, which is in fact \$3.3\times100\$.
Finally, our corrected output needs to be scaled back. We just multiply by the previously computed multiplier.

Images

E24 from 100 to 1000 in steps of 5

E48 from 100 to 1000 in steps of 5

E96 from 100 to 1000 in steps of 5

E192 from 100 to 1000 in steps of 5

Alternative with single equation

Named cell	Equation in code style, other in italics	Value (Example)
Input	Data Input	332.5
Target	Dropdown cell with values: 24, 48, 96, and 192	24
Output	`=10^INT(LOG10(Input))IF(Target<>24; ROUND(POWER(10^ROUND(TargetLOG10(Input/10^INT(LOG10(Input))); 0); 1/Target); IF(Target=24; 1; 2)); XLOOKUP(0; ABS({1;1.1;1.2;1.3;1.5;1.6;1.8;2;2.2;2.4;2.7;3;3.3;3.6;3.9;4.3;4.7;5.1;5.6;6.2;6.8;7.5;8.2;9.1} - Input/10^INT(LOG10(Input))); {1;1.1;1.2;1.3;1.5;1.6;1.8;2;2.2;2.4;2.7;3;3.3;3.6;3.9;4.3;4.7;5.1;5.6;6.2;6.8;7.5;8.2;9.1};; 1))`	330

Ah yes, I forgot to mention.that my answer is a replacement for the top-voted answer's VBA function for a single input. Of course, this can be extended to a table nontheless. I usually prefer not to use VBA whenever I can. — StickySli, Sep 13 '23 at 14:08
So this is a pretty neat approach to finding the E series resistor value for a desired resistor. A few comments: When I paste this into Excel, the semicolon/comma swap doesn't work for me - I had to change most of the semicolons to commas for Excel to recognize the equations properly. Second, you should probably be using FLOOR on Index_Rounded, if you're looking for the closest value - putting 332 in Input for an E24 gives me 360 instead of 330. Finally, the original post is about finding ratios, not single E-series resistors. — W5VO, Sep 13 '23 at 15:38
I agree, this code is really neat for finding the nearest value in the E-series. I definitely learnt something. But I think there is still a tiny bug in the formula. It works in the range [1.0 < x <= 4.7]. After that some intermediate values are skipped: see https://i.stack.imgur.com/73Qol.png — Velvet, Sep 13 '23 at 15:54
@Velvel I have solved the problem. The culprit was the legacy LOOKUP. I since swapped it with XLOOKUP to round to the nearest E24 value. A 2nd table was added for the E24_Series values to declutter the equations. — StickySli, Sep 14 '23 at 00:35
Not going to edit this anymore, but if you need to compare the upper and lower resistor values, for the upper resistor value, just change the ROUND to ROUNDUP, and for the lower resistor value change ROUND for ROUNDDOWN and also change the XLOOKUP's match mode parameter from 1 to -1. You can find an example in this 24 step attenuator calculator I made. — StickySli, Sep 17 '23 at 13:04

score 2 · Answer 3 · answered Sep 06 '22 at 04:50

I have faced this tricky little problem many times in my career, and eventually ended up with the solution of putting the E24 series (and 48, 96 and 192) into a spreadsheet. When I want to find a ratio, I fill in the 'ratio' cell, and the 'series' x 'ratio' column updates. Then I scan my eye down that column to look for integer or near integer results. The biggest drawback with that method is remembering where I archived it from last use.

You're unlikely to find E24 components in better than 1% tolerance. For many purposes anyway, that's good enough. Don't let the 'perfect' be the enemy of 'meets specification'.

Resistors are dirt cheap. If you aim to use three from the start, choose a 'shim' resistor nominally 10x the value of one of the others, and when your main resistor ratio is close, adjust the parallel shim to bring it closer. Or you could choose a /10 resistor in series, whichever is more convenient.

Thank you for more illumination on the topic. Though all I needed was the spreadsheet shared above, so one does not have to do the same work, which you people already invested. — Paul Smith, Sep 06 '22 at 21:01

score 1 · Answer 4 · answered Sep 13 '23 at 15:13

Here's my go-to Mathematica tabulator for this:

ratio = 257/42;
maxError = 0.01;
e24ratios = {1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 
   2.4, 2.7, 3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8, 7.5, 
   8.2, 9.1};
e24values = Map[# {1^3, 10^3, 100*^3} &, e24ratios] // Flatten;
ratios = Map[{#[[1]]/#[[2]], #} &, Permutations[e24values, {2}]];
errorF[r_] := (r[[1]] - ratio)/ratio
values = Select[ratios, Abs[errorF[#]] <= maxError &];
Block[{$NumberMarks = False},
    StringForm["|1|2|3|\n", 
     NumberForm[#[[1]], 2], #[[2, 1]], #[[2, 2]]]] & /@
  ({errorF[#]*100, #[[2]]} & /@ values // SortBy[First]);
ToString /@ % // StringJoin // "|Error|R1|R2|\n|-|-|-|\n" <> # &

Error	R1	R2
-0.96	20000.	3300.
-0.96	200000.	33000.
-0.86	9100.	1500.
-0.86	910000.	150000.
-0.86	91000.	15000.
-0.13	11000.	1800.
-0.13	22000.	3600.
-0.13	110000.	18000.
-0.13	220000.	36000.
0.57	240000.	39000.
0.57	560000.	91000.
0.57	24000.	3900.
0.57	56000.	9100.